Invariance modulaire
En théorie des cordes, l'invariance modulaire correspond à la contrainte imposée sur la fonction de partition de tout modèle d'être inchangée sous l'effet d'une transformation modulaire de la feuille d'univers.
Catégories :
Théorie des cordes - Gravité quantique - Physique quantique
Recherche sur Google Images :
Source image : fr.wikipedia.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- riance conforme de la théorie formulée sur la feuille d'univers, et l'invariance modulaire de la fonction à une boucle. Nous verrons que la dimension de ... (source : tel.archives-ouvertes)
En théorie des cordes, l'invariance modulaire correspond à la contrainte imposée sur la fonction de partition de tout modèle d'être inchangée sous l'effet d'une transformation modulaire de la feuille d'univers.
Le plus fréquemment on considère le cas de la fonction de partition à une boucle pour laquelle la feuille d'univers est topologiquement un tore. Dans ce cas les transformations modulaires correspondent aux difféomorphismes globaux du tore qui forment le groupe modulaire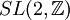 
.
L'invariance modulaire assure l'absence d'anomalie gravitationnelle pour la théorie conforme définie sur la feuille d'univers.
Sources
- (en) J. Polchinski, String theory [détail des éditions]
- (en) M. B. Green, J. H. Schwarz et E. Witten, Superstring theory [détail des éditions]
Recherche sur Amazone (livres) : |
Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Invariance_modulaire.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.
Accueil
Recherche
Début page
Contact
Imprimer
Accessibilité