Inégalités de Bell

En mécanique quantique, les inégalités de Bell sont les relations que doivent respecter les mesures sur des états intriqués dans l'hypothèse d'une théorie déterministe locale à variables cachées.

Catégories :

Mécanique quantique - Physique quantique

Source image : perso.ens-lyon.fr
Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur.

Page(s) en rapport avec ce sujet :

Si on mesure la même grandeur pour les deux particules d'un même couple les ... par conséquent les inégalités de Bell et invalide toute théorie à variables cachées.... (source : edgar-bonet)
Inégalités de Bell. Les mesures ne sont pas obligatoirement semblables sur les deux particules. A titre d'exemple, on peut mesurer le spin d'une des particules... (source : techno-science)
de particules, predit par la theorie quantique, nomme alors (etat EPR), .... Trois tests experimentaux des inegalites de Bell par une mesure de ... (source : psychosmose.free)

En mécanique quantique, les inégalités de Bell (du nom de leur auteur : John Stewart Bell) sont les relations que doivent respecter les mesures sur des états intriqués dans l'hypothèse d'une théorie déterministe locale à variables cachées. Jusqu'désormais, l'expérience démontre que les inégalités de Bell sont toujours violées, nous forçant à renoncer à une des deux hypothèse suivantes :

Un signal ne peut aller plus vite que la vitesse de la lumière dans le vide.
Un objet ne peut occuper qu'un seul lieu de l'espace à un instant donné (principe de localité).

États intriqués

Article détaillé : Intrication quantique.

Deux particules sont dites dans un état intriqué quand l'état des deux particules n'est pas factorisable en un produit tensoriel de deux états à une particule. Cela peut être obtenu par exemple quand une particule se scinde en deux particules semblables. Les lois de conservation amènent à des valeurs semblables ou strictement opposées des propriétés de ces deux particules tels que l'impulsion ou le moment angulaire (l'état de spin).

Ce type de situation est décrit dans le paradoxe EPR.

Quand on effectue une même mesure, par exemple la mesure du spin dans une direction donnée, sur deux particules intriquées on obtient deux résultat correllés (deux résultats semblables dans le cas du spin d'un photon).

Classiquement cela est particulièrement normal puisque ces deux particules sont semblables. Mais du point de vue de la mécanique quantique cela peut sembler paradoxal puisque les résultats des mesures sont probabilistes. Ainsi, une particule dans un état non polarisé peut être mesurée avec un spin vertical ou horizontal avec une chance sur deux. Et des mesures successives sur des particules dans le même état donneront des résultats différents. Cependant, quoique les résultats soient localement aléatoires pour chacune des deux particules, on observe toujours une corrélation entre les deux résultats.

En réalité, cela n'est pas en contradiction avec la mécanique quantique car il faut bien s'entendre sur la signification du terme "même état". Dans le cas de particules successives indépendantes, il s'agit plutôt d'états identiques. Alors que dans le cas de deux particules intriquées c'est un seul et même état décrivant les deux particules.

Dans le cas de deux particules indépendantes, on décrira l'état comme :

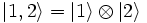
$\left| 1,2 \right\rangle = \left| 1 \right\rangle \otimes \left| 2 \right\rangle$

Tandis que dans le cas intriqué une telle décomposition n'est pas envisageable.

Les différentes possibilités

Le résultat d'une mesure n'est pas complètement inscrit dans l'état de la particule puisque les résultats ont une nature probabiliste. Cependant la mesure sur les deux particules donne bien le même résultat. Quelle est la nature du lien garantissant le fait que le résultat sera le même ? Plusieurs hypothèses sont envisageables.

Théories non locales

Dans ce cas on émet l'hypothèse qu'un signal instantané (de nature inconnue) autorise une particule d'être informée du résultat d'une mesure sur l'autre particule. Certaines variantes de l'expérience d'Aspect montrent que ce signal devrait même remonter le temps dans le référentiel d'une des deux particules.

Variables cachées

L'hypothèse précédente présente l'inconvénient d'être en désaccord avec la relativité restreinte. De plus, le comportement probabiliste de la mécanique quantique peut être perçu comme une anomalie de cette théorie. Une solution consiste à émettre l'hypothèse que la description quantique de l'état est incomplète. Il existerait des variables cachées qui déterminent de manière univoque le résultat d'une mesure. Comme dans un raisonnement classique, ce n'est que l'ignorance de la valeur exacte de ces variables qui donne un comportement probabiliste. Le lien entre les particules intriquées devient superflu car le fait qu'elles soient complètement semblables garantit que leurs variables cachées ont même valeur et par conséquent que les mesures donnent le même résultat.

Les inégalités de Bell modélisent la statistique des corrélations associées à ce type de théories. Leur violation montrent par conséquent que l'intrication ne peut être décrite par une théorie locale à variables cachées.

Mécanique quantique

La troisième possibilité est d'admettre la mécanique quantique telle qu'elle est . De dire que les mesures sont réellement probabilistes et les états intriqués correctement décrits par la mécanique quantique. Cela peut poser de gros problèmes d'interprétations qui ne sont d'ailleurs pas entièrement résolus à notre époque. La nature du "lien" entre les deux particules reste assez complexe à saisir (voir Conclusions).

Multivers (théorie d'Everett)

Selon cette théorie, il n'est pas besoin de faire appel à des variables cachées ni à une transmission d'information d'état d'une particule vers une autre : l'ensemble des couples d'états valides, pour les deux particules, existent simultanément dans des réalités parallèles. Le fait pour un observateur d'effectuer une mesure le fait entrer dans une des ces réalités, lui donnant l'impression que l'état des deux particules est affecté simultanément malgré la distance qui les sépare. ^[1] Cette solution entre dans la catégorie "théorie à variables cachées non-locales", la variable cachée étant "dans quelle branche d'univers sommes nous ?".

Inégalités de Bell

Les mesures ne sont pas obligatoirement semblables sur les deux particules. A titre d'exemple, on peut mesurer le spin d'une des particules selon un certain angle et le spin de l'autre particule selon un autre angle.

Les résultats des mesures sont alors de nature statistique. A titre d'exemple, la mesure du spin avec un polariseur donne toujours un résultat tout ou rien. Ce qu'on obtiendra alors pour les deux mesures sont des statistiques de coïncidences : les deux mesures donnent un résultat semblable dans X% des cas (et non 100% dans le cas de mesures semblables). La plupart de mesures successives (sur la plupart de paires de particules) permet alors de calculer la corrélation entre ces mesures de spin sous des angles différents.

Si on se place dans l'hypothèse des théories locales déterministes à variables cachées, les inégalités de Bell donnent des relations auxquelles ces corrélations doivent obéir.

Nous allons démontrer ces inégalités dans un cas légèrement plus simple que celui d'un angle quelconque pour bien montrer l'origine du raisonnement.

Soit deux particules $α$ et $β$ dont le spin a trois composantes $A$ , $B$ et $C$ . Les composantes peuvent prendre deux valeurs + et -. Pour chaque composante, nous noterons les valeurs $A +$ , $B -$ , etc. Les deux particules ont des spins opposés. Quand $α$ a la composante $A +$ , alors $β$ a la composante $A -$ , etc.

On mesure des paires de valeurs $A B$ , $A C$ et $B C$ sur les deux particules. Le résultat des mesures est désigné par $A + C -$ , etc.

Si l'état des particules est déterministe, décrit par des variables cachées, alors chaque particule a un spin idéalement déterminé avec des composantes $A$ , $B$ et $C$ précises. Même si les variables cachées ne sont pas connues avec exactitude, et par conséquent le spin, il n'empêche que cette valeur précise existe.

Soit un ensemble de particules dans un état de spin donné pris dans un ensemble plus vaste, quelconque, de particules dans l'ensemble des états envisageables. Par exemple 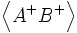$\left\langle Aˆ+Bˆ+ \right\rangle$ est la totalité des particules avec ces composantes, 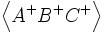$\left\langle Aˆ+Bˆ+Cˆ+ \right\rangle$ la totalité des particules avec ces composantes, ...

Alors nous aurons :

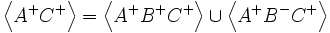
$\left\langle Aˆ+Cˆ+\right\rangle = \left\langle Aˆ+Bˆ+Cˆ+\right\rangle\cup\left\langle Aˆ+Bˆ-Cˆ+\right\rangle$

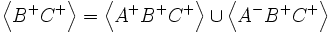
$\left\langle Bˆ+Cˆ+\right\rangle = \left\langle Aˆ+Bˆ+Cˆ+\right\rangle\cup\left\langle Aˆ-Bˆ+Cˆ+\right\rangle$

Ces relations découlent tout simplement de la théorie des ensembles.

Donc :

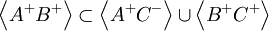
$\left\langle Aˆ+Bˆ+\right\rangle\subset\left\langle Aˆ+Cˆ-\right\rangle\cup\left\langle Bˆ+Cˆ+\right\rangle$

Si 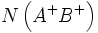$N\left( Aˆ+Bˆ+\right)$ sert à désigner le nombre de particules dans cet état, alors :

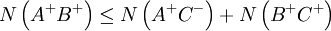
$N\left( Aˆ+Bˆ+\right) \le N\left( Aˆ+Cˆ-\right) + N\left( Bˆ+Cˆ+\right)$

Maintenant, nous effectuons nos mesures sur deux particules de spins opposés et ces particules sont émises sous forme d'un flux de particules de spins quelconques. Nous en déduisons que :

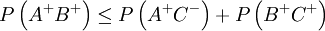
$P\left( Aˆ+Bˆ+\right) \le P\left( Aˆ+Cˆ-\right) + P\left( Bˆ+Cˆ+\right)$

où 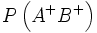$P\left(Aˆ+Bˆ+\right)$ est la probabilité de mesurer $A +$ sur l'une des particules et $B +$ sur l'autre.

C'est un exemple d'inégalité de Bell.

Dans le cas de la mesure du spin selon un angle quelconque, on n'utilise que deux composantes du spin et l'angle entre les composantes. Le calcul est légèrement plus compliqué mais identique. Le résultat est :

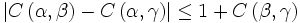
$\left| C\left(\alpha,\beta\right) - C\left(\alpha,\gamma\right)\right| \le 1 + C\left(\beta,\gamma\right)$

où $α$ , $β$ et $γ$ sont des angles donnés aux polariseurs et 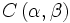$C\left(\alpha,\beta\right)$ est la fonction de corrélation pour ces deux angles (la corrélation peut être négative).

La mécanique quantique

Dans le cas de la mécanique quantique, si l'angle du premier polariseur est $α$ et l'angle du deuxième polariseur est $β$ , alors le calcul (semblable à la probabilité de mesurer le spin selon l'angle $α$ tandis qu'on sait que le spin a été mesuré selon l'angle $β$ ) donne :

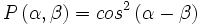
$P\left(\alpha,\beta\right) = cosˆ2\left(\alpha-\beta\right)$

Comme on mesure des coïncidences, la fonction de corrélation est alors donnée par :

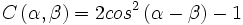
$C\left(\alpha,\beta\right) = 2 cosˆ2\left(\alpha-\beta\right) - 1$

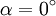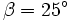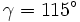On voit que les inégalités de Bell sont violées pour, par exemple, des angles égaux à $\alpha=0ˆ\circ$ , $\beta=25ˆ\circ$ et $\gamma=115ˆ\circ$ .

L'expérience (par exemple celle d'Alain Aspect) a beaucoup confirmé ces résultats et aussi que la loi de Malus était vérifiée sur des photons individuels.

Conclusions

Comme les inégalités de Bell sont expérimentalement violées (si elles sont correctes), cela veut dire qu'il est impossible de construire une théorie locale déterministe à variables cachées rendant compte des résultats expérimentaux.

Cela n'interdit pas la construction de théories déterministes non locales à variables cachées quoique le fait que la mécanique quantique n'ait jamais été mise en défaut semble rendre peu utile une telle recherche. Un des fondateurs de la physique quantique, Louis De Broglie, a ainsi proposé une modélisation des ondes quantiques vérifiant à la fois déterminisme et inégalités de Bell. Cependant la majorité des théories explicitement non locales (signaux instantanés) sont en contradiction avec la relativité restreinte et il est intéressant de signaler que la relativité restreinte et la mécanique quantique se marient particulièrement bien. D'autres résultats comme le théorème de Kochen-Specker renforcent cette attitude.

Il reste que la mécanique quantique est curieuse car elle implique manifestement un lien entre les deux particules analogue à la conservation du moment cinétique. Lien qui n'est pas explicite dans des variables internes dont nous ignorerions l'existence. Ce lien est quelquefois qualifié "d'instantané" quoique ce terme soit impropre dans la mesure où il ne s'agit pas d'un transfert d'information. On montre d'ailleurs généralement que l'intrication quantique ne permet pas de transférer de l'information entre les deux particules par quelque système de mesure que ce soit^[2].

Dans le cas qui nous préoccupe, c'est même assez évident puisque le résultat d'une mesure sur une particule individuelle est complètement aléatoire. Si le fait de mesurer une particule induit le résultat sur l'autre particule, le résultat sur cette deuxième particule n'en reste pas moins aléatoire puisque la mesure sur la première l'est aussi. Ce n'est qu'en comparant les résultats des deux mesures qu'on pourra constater une corrélation et par conséquent un lien (l'intrication). Et cette comparaison ne pourra se faire que via un canal classique de transfert d'informations.

L'absence de transfert d'information quantique n'empêche pas l'exploitation de cet effet par exemple dans la cryptographie quantique. L'absence de variables cachées et la possibilité d'exploiter l'intrication montre par conséquent que ce lien est effectif. L'existence d'un lien non local sans transfert de signal (respectant par conséquent la localité relativiste) est complètement sans équivalent classique, ce qui la rend assez mystérieuse^[3].

Une partie des difficultés à comprendre la nature du phénomène est probablement liée à notre intuition profondément classique. Il est particulièrement complexe de raisonner autrement qu'en termes de "deux" particules comme si c'était des entités scindées avec un certain lien entre elles. Tandis que l'intrication montre clairement que les particules ne sont pas séparables. On devrait par conséquent plutôt raisonner comme si c'était une paire de particules. Le mot "paire" étant pris dans le sens : "un et un seul objet". Cela rend l'effet moins problématique mais pas moins mystérieux car on remplace uniquement la notion de "lien non local" par celle "d'objet non local". ^{[citation nécessaire]}

Cette vision séparatiste donnant l'impression d'un lien instantané est fortement consolidée par l'interprétation de Copenhague de la mécanique quantique. Même si ce n'est pas l'unique, c'est l'interprétation la plus commune et la plus naturelle en ce qu'elle est une image directe du comportement probabiliste des mesures expérimentales.

Dans le cadre de cette interprétation, la mesure sur une particule "réduit" sa fonction d'onde qui ne prend alors plus qu'une seule valeur envisageable : celle mesurée. Comme les particules sont intriquées, l'autre particule voit aussi sa fonction d'onde réduite instantanément.

Mais la mécanique quantique n'a pas obligatoirement besoin d'une telle interprétation. Celle-ci n'a d'usage que pratique. Et les difficultés (voir par exemple le chat de Schrödinger) de l'interprétation de Copenhague montrent que cette réduction ne doit pas être obligatoirement vue comme un processus physique effectif. Le fait qu'elle soit instantanée est alors troublant mais n'est plus un problème physique. ^{[citation nécessaire]}

Quoi qu'il en soit, le problème de l'interprétation de la violation des inégalités de Bell, de l'intrication et de la mécanique quantique généralement est un problème complexe et le débat reste ouvert.

Travaux originaux

J. S. Bell, On the Einstein Podolsky Rosen Paradox, Physics 1 (1964), 195.

J. S. Bell, On the problem of hidden variables in quantum mechanics, Review of Modern Physics 38 (1966), 447.

J. S. Bell, Introduction to the hidden variable question, Proceedings of the Mondial School of Physics Enrico Fermi, Course IL, Foundations of Quantum Mechanics (1971), 171-181.

J. S. Bell, Speakable and Unspeakable in Quantum Mechanics, Cambridge University Press (1987), ISBN

M. Bell, K. Gottfried & M. Veltman ; John S Bell on the foundations of quantum mechanics, World Scientific (2001), ISBN 981-02-4688-9.

Autres références

Banesh Hoffmann, Michel Paty, L'étrange histoire des quanta, Editions du seuil, 1981.

Alain Aspect ; Quelques tests expérimentaux des fondements de la mécanique quantique (en optique) , Qu'est-ce que l'Univers ?, Vol. 4 de l'Université de L'ensemble des Savoirs (sous la direction d'Yves Michaux), Odile Jacob (2001), ISBN 2-7381-0917-9, pp. 589. Dualité onde-corpuscule, intrication quantique & paradoxe EPR expliqués par un professeur d'optique à l'Université de Paris-Sud (Orsay), auteur en 1982 d'une expérience testant les inégalités de Bell.
Alain Aspect ; Bell's Theorem : The naive view of an experimentalist, conférence en mémoire de John Bell (Vienne, Décembre 2000). Publié dans : R. A. Bertlmann et A. Zeilinger (eds. ) ; Quantum [un]speakables - From Bell to quantum information, Springer (2002). Texte complet disponible sur l'ArXiv : quant-ph/0402001.

R. Jackiw, A. Shimony ; The depth and breadth of John Bell's physics, Phys. Perspect. 4 (2004) 78-116. Texte complet disponible sur l'ArXiv : physics/0105046.

Asher Peres ; All the Bell inequalities, Foundations of Physics 29 (1999) 589-614. Texte complet disponible sur l'ArXiv : quant-ph/9807017.

H. M. Wiseman ; From Einstein's theorem to Bell's theorem : a history of quantum nonlocality, Contemporary Physics 47, 79-88 (2006) ; texte complet disponible sur l'ArXiv : quant-ph/0509061 (Septembre 2005).

Liens externes

Notes

↑ The Everett FAQDœs the EPR experiment prohibit locality? What about Bell's Inequality?
↑ A. Aspect Expériences basées sur les inégalités de Bell. J. Physique Colloque C2, 940 (1981)
↑ Voir Expérience d'Aspect et l'ensemble des efforts réalisés pour éliminer toute source envisageable de corrélation "classique"

Recherche sur Amazone (livres) :

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/In%C3%A9galit%C3%A9s_de_Bell.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.