Variété de Calabi-Yau

Une variété de Calabi-Yau, ou espace de Calabi-Yau est un type spécifique de variété en mathématiques intervenant dans des domaines comme la géométrie algébrique mais également en physique théorique et surtout dans la théorie des supercordes où elles jouent le rôle d'espace de compactification. C'est dans le cadre de l'étude de ces variétés qu'a eu lieu l'une des plus importantes collaborations entre physiciens et mathématiciens qui a abouti à la découverte de la symétrie miroir qui établit une relation non-triviale entre deux variétés de Calabi-Yau dont les topologies peuvent être différentes. La définition précise de ces variétés est particulièrement technique. Elle sera exposée plus bas.

Définition formelle

Une variété de Calabi-Yau est définie comme une variété kählérienne dont la première classe de Chern est nulle. Le mathématicien Eugenio Calabi a conjecturé en 1957 que de telles variétés admettent obligatoirement une métrique dont le tenseur de Ricci s'annule (on parle aussi d'espace Ricci-plat). La conjecture a été démontrée par Shing-Tung Yau en 1977 dans ce qui est devenu le théorème de Yau. Par conséquent, on peut aussi définir une variété de Calabi-Yau comme un espace compact, Kähler et Ricci-plat.

De façon toujours équivalente, un espace de Calabi-Yau de dimension complexe 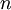(ce qui correspond à une dimension réelle 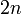) peut être vu comme une variété riemannienne d'holonomie réduite à 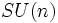(le groupe d'holonomie d'une variété riemannienne de dimension réelle 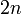étant génériquement le groupe ).

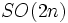Enfin, on peut toujours voir de façon équivalente un espace de Calabi-Yau comme une variété kählérienne admettant une 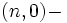forme holomorphe définie globalement et ne s'annulant nulle part. Cette dernière condition est équivalente à ce que le fibré canonique sur la variété soit trivial. Ceci se traduit par une classe canonique triviale. Ce dernier point de vue est utile pour généraliser la définition d'une variété Calabi-Yau au cas d'espaces possédant des singularités car même si la classe de Chern n'est pas bien définie pour un espace singulier on peut toujours considérer les notions de fibré canonique et de classe canonique.

Il est notable cependant que même pour certains des Calabi-Yau les plus simples (voir plus bas) on ne sait pas exhiber explicitement la métrique Ricci-plate quoique son existence soit assurée par le théorème de Yau.

Exemples de variétés de Calabi-Yau

• En dimension complexe 1 l'unique variété Calabi-Yau est le 2-tore.
• En dimension complexe 2 il n'existe que deux variétés Calabi-Yau à isomorphisme près. Il s'agit du 4-tore et de l'espace K3. Sur ce dernier, aucune métrique Ricci-plate explicite n'est connue. Il en va de même pour l'ensemble des Calabi-Yau de dimensions supplémentaires non-triviaux.
• À partir de la dimension complexe 3 (dimension réelle 6) le nombre de Calabi-Yau devient illimité et il n'existe pas toujours de classification générale. On peut en construire cependant un grand nombre qui possèdent en plus la propriété d'être des variétés toriques.

Usage en principe des cordes

Les variétés Calabi-Yau sont spécifiquement utilisées en théorie des supercordes car elles préservent une partie de la supersymétrie de la théorie originale à 10 dimensions sous le processus de réduction dimensionnelle pour obtenir une théorie effective à 4 dimensions. En plus des propriétés phénoménologiques intéressantes de la supersymétrie (surtout pour expliquer la faiblesse de la constante cosmologique), l'existence de la supersymétrie au niveau de la théorie effective simplifie l'étude formelle des modèles envisagés car nombre de constantes de couplage sont protégées de corrections perturbatives ou non-perturbatives par l'intermédiaire de théorème de non-renormalisation. Leur détermination à l'ordre des arbres dans l'expansion diagrammatique^[1] de la théorie est alors suffisante pour connaître leur valeur dans la théorie effective.

Description

La complexité de cette variété est telle qu'elle ne peut pas être représentée précisément. Elle contiendrait à elle seule six dimensions, raison pour laquelle de tels replis et déformations apparaissent. Car c'est bien de la compression de la variété que découle cette complexité en 2 dimensions. Quand elle est utilisée comme dimension enroulée, la taille d'une variété de Calabi-Yau vaut la longueur de Planck, soit 10^-33cm.

Transitions de géométrie

Il est remarquable que au contraire de l'intuition classique, la théorie des cordes puisse donner des résultats équivalents au niveau de la théorie effective à 4 dimensions quand elle est compactifiée sur deux variétés différentes. Quelquefois ces deux variétés Calabi-Yau peuvent même avoir des topologies différentes. On parle alors de transition géométrique. Des exemples spécifiques de telles transitions sont donnés par la transition de flop et la transition de conifold.

Symétrie miroir

Point de vue mathématique

Notes

1. ↑ il est quelquefois indispensable de pousser le développement jusqu'à l'ordre d'une boucle.

Liens externes

Quelques exemples de variétés Calabi-Yau :

• [1]
• [2]
• [3]
• [4]

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Vari%C3%A9t%C3%A9_de_Calabi-Yau.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.