Diffusion Compton
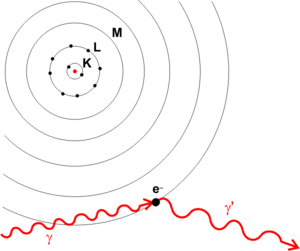
En physique, la diffusion Compton est la diffusion d'un photon sur une particule de matière, comme un électron. On nomme effet Compton plus particulièrement l'augmentation de la longueur d'onde du photon par la diffusion.

Catégories :
Optique quantique - Électrodynamique quantique - Théorie quantique des champs - Physique quantique
En physique, la diffusion Compton est la diffusion d'un photon sur une particule de matière, comme un électron. On nomme effet Compton plus particulièrement l'augmentation de la longueur d'onde du photon par la diffusion. Ce dernier phénomène a été observé la première fois par Arthur Compton en 1923. L'expérience de Compton devint l'ultime observation qui convainquit l'ensemble des physiciens que la lumière peut se comporter comme un faisceau de particules dont l'énergie est proportionnelle à la fréquence (ou inversement à la longueur d'onde). Cet effet est important en physique car il a démontré que la lumière ne peut pas être seulement décrite comme une onde, ni comme une particule.
Histoire de la découverte de l'effet Compton
C'est dans une atmosphère de particulièrement grand scepticisme au sujet de la théorie de la quantification de la lumière d'Albert Einstein qu'Arthur H. Compton commence ses travaux de thèse (Ph. D. ) en 1912, thèse qu'il soutiendra à l'université de Princeton en juin 1916. Il passe l'année suivante (1916-1917) comme professeur de physique à l'université du Minnesota, puis devient ingénieur de recherche pour la compagnie des lampes Westinghouse durant 2 ans (1917-1919). Arthur Compton reçoit en 1919 une des premières bourses du conseil national de la recherches pour aller étudier en Grande-Bretagne à Cambridge, au sein du laboratoire Cavendish pour l'année universitaire 1919-1920. De retour aux États-Unis, il est appelé Professeur de Physique et Directeur du département de Physique de l'université Washington à Saint Louis, Missouri. Il y reste jusqu'en 1923, date de la publication de sa découverte de l'effet qui porte désormais son nom.
Quand Compton commence ses recherches à l'université du Minnesota en 1916, l'électrodynamique classique est toujours acceptée par une très grande majorité des physiciens. Compton voulait tester expérimentalement une ancienne théorie de Wilhelm Weber considérant l'atome comme l'ultime particule magnétique. Pour cette expérience, Compton fit réfléchir des rayons X sur un cristal de magnétite en ajoutant alternativement un champ magnétique extérieur. Il cherchait à observer un éventuel changement dans les figures de diffraction de Max von Laue, qui auraient dû apparaître du fait du mouvement des atomes de magnétite dans leur réseau cristallin. Malgré de nombreuses tentatives, Compton ne vit jamais de modification des figures de diffraction. Il passe alors les cinq années suivantes à essayer de comprendre comment les rayons X étaient diffusés quand ils traversent la matière.
Quand il rejoint la compagnie Westinghouse en 1917, ces résultats l'avaient déjà convaincu que ce n'était pas l'atome qui était la particule magnétique ultime mais bien l'électron. Durant sa période industrielle, Compton continue à travailler sur des sujets théoriques concernant la dimension de l'électron. Compton réfléchit à de nouvelles idées à Cavendish, non seulement grâce aux critiques nombreuses de Rutherford, mais également grâce aux résultats expérimentaux qu'il a pu obtenir pendant son séjour à Cavendish.
Ses expériences les plus significatives sont identiques à celles que J. A. Gray a effectuées à Cavendish avant la Première Guerre mondiale. Elles consistaient à envoyer un faisceau de rayons gamma sur des feuilles minces de diverses substances telles que le fer, l'aluminium et la paraffine, en plaçant un écran en premier lieu dans le faisceau primaire puis dans le faisceau secondaire, pour observer s'il y avait des différences entre les rayons gamma dans les deux faisceaux.
Compton constate qu'en effet des différences existent. Les rayons gamma secondaires ou diffusés sont plus intenses vers l'avant que vers l'arrière. En d'autres termes ils sont «plus mous» ou d'une plus grande longueur d'onde que les rayons gamma primaires. Cette «dureté» ou longueur d'onde ne dépend pas de la nature du matériau diffuseur et elle devient «plus molle» (ou d'une plus grande longueur d'onde) quand l'angle de diffusion est plus grand.
Une nouvelle fois, Compton suppose que la longueur d'onde des rayons gamma ne peut pas être modifiée lors de la diffusion – conformément à la théorie classique de diffusion de Thomson. Il a par conséquent recherché une nouvelle explication. Compton finit par conclure que les rayons gamma primaires excitaient l'émission d'un nouveau type de rayonnement gamma de fluorescence dans le matériau diffuseur - un nouveau type parce que l'unique des quatre caractéristiques que ce rayonnement avait en commun avec le rayonnement de fluorescence classique était qu'il avait une plus grande longueur d'onde que le rayonnement primaire. Mais comment un type de rayonnement fluorescent si nouveau pouvait-il être excité dans le matériau diffuseur?
Compton proposa un mécanisme spécifique : les rayons gamma primaires frappent les électrons dans le diffuseur, qu'il considère désormais comme des oscillateurs électriques, et sont propulsés vers l'avant à des vitesses relativistes. Le rayonnement émis formerait un pic dans la direction vers l'avant, et lors de son observation perpendiculairement à la direction du mouvement, il subirait un décalage Doppler induisant une plus grande longueur d'onde que le rayonnement primaire. C'est ainsi que Compton expliqua les caractéristiques des rayons gamma diffusés qu'il avait observés.
Quand Compton quitta le laboratoire de Cavendish à la fin de l'été 1920 pour prendre la charge de professeur à l'université Washington à Saint Louis, Missouri, il emporta avec lui un spectromètre de Bragg, dans l'objectif de voir si les rayons X pourraient exciter le même nouveau type de rayonnement fluorescent - avec toutes ses caractéristiques peu communes qu'il avait observées pour les rayons gamma. Son plan était d'utiliser son spectromètre de Bragg non pas comme spectromètre, mais comme «sélecteur de longueur d'onde», c'est-à-dire pour produire un faisceau monochromatique de rayons X. En avril 1921 il obtint sa réponse : les rayons X monochromatiques excitaient en effet le même nouveau type de rayonnement fluorescent que les rayons gamma. En outre, comme il le découvrit bientôt avec Charles F. Hagenow, le nouveau rayonnement de fluorescence X est aussi polarisé – un nouveau comportement surprenant comparé au rayonnement de fluorescence ordinaire.
À l'automne 1921, Compton a une nouvelle surprise. J. A. Gray, désormais à l'université McGill à Montréal mais qui travaillait provisoirement dans le laboratoire de William H. Bragg à l'université de Londres, s'était aussi tourné vers des expériences de rayons X en 1920. Il avait envoyé des rayons X approximativement homogènes d'une raie de l'étain sur un écran en aluminium et avait aussi constaté que les rayons X secondaires étaient bien plus «mous» que les primaires. Il expliqua cette observation en supposant que les rayons X primaires se composaient d'impulsions électromagnétiques interférant les unes avec les autres après avoir été diffusées, pour former des impulsions plus larges, c'est-à-dire plus «douces». En même temps, Gray invoquait aussi que si ses rayons de X primaires étaient constitués non pas d'impulsions électromagnétiques mais d'ondes électromagnétiques véritablement monochromatiques, alors les rayons X secondaires ou diffusés auraient obligatoirement la même longueur d'onde que les primaires - suivant toujours la théorie classique de la diffusion de Thomson. En septembre 1921, S. J. Plimpton, qui travaillait aussi dans le laboratoire de Bragg à Londres, confirma l'interprétation de Gray. Plimpton montra qu'un faisceau homogène de rayons X, produits par réflexion à partir d'un cristal incurvé de mica, ne devenait pas plus «mou» une fois diffusé par de la paraffine ou de l'eau.
L'interprétation de Gray et la confirmation de Plimpton troublèrent profondément Compton, parce qu'il avait conclu que lorsque un faisceau primaire homogène de rayons X traversait la matière, le secondaire ou les rayons X diffusés étaient en effet plus «mous» que les primaires, dans la mesure où ils étaient composés de son nouveau type de rayons X de fluorescence. Alors, Compton, immédiatement (en octobre 1921), effectua d'autres expériences et fut convaincu que Plimpton était dans l'erreur et que lui avait raison. Compton considéra son expérience comme principale – crucis experimentum, dans la terminologie vénérable de Newton - entre la sienne et les théories de Gray, n'ayant pas la moindre idée qu'une troisième théorie entièrement différente était alors envisageable.
Juste après avoir rapporté les résultats qui ont précédé, Compton fait le plus consécutif de l'ensemble des changements dans son programme expérimental. Il commence à utiliser son spectromètre de Bragg non plus comme «sélecteur de longueur d'onde» mais comme véritablement un spectromètre, c'est-à-dire qu'il commence à comparer le spectre du rayonnement secondaire et celui des rayons X primaires. Il utilise pour ses rayons X primaires la raie K du molybdène, dont la longueur d'onde est λ = 0, 708 Angströms, qu'il envoie sur des diffuseurs de pyrex et de graphite. Il observe alors les rayons X secondaires à un angle de diffusion d'environ 90 degrés.
Il publie ses résultats dans Physical Review au début de décembre 1921. Il ne montre pas les spectres obtenus dans cet article, mais ses cahiers d'expérience, retrouvés depuis, montrent que la raie du spectre secondaire est décalée un peu vers la droite de celle du spectre primaire, ce que Compton n'a pas vu à ce moment. Son article stipule que la longueur d'onde du rayonnement secondaire est de 0, 95 Angström, ou à peu près 35% plus grande que celle du spectre primaire à 0, 708 Angström. En d'autres termes, Compton considère que le spectre primaire est constitué des raies intenses à gauche – vu comme une raie simple à 0, 708 Å - et que le spectre secondaire était les raies plus petites à droite - vu comme raie simple à 0, 95 Angström. Le rapport mesuré des longueurs d'onde primaire/secondaire était alors λ / λ'= 0, 708/0, 95 = 0, 75.
À partir de ces données, Compton explique cette grande variation dans la longueur d'onde en utilisant son hypothèse du rayonnement de fluorescence et interprète le grand décalage de longueur d'onde comme un effet Doppler. Ainsi, vu à un angle de 90°, le rapport des longueurs d'onde primaire/secondaire est donné près 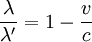 , où v est la vitesse des électrons-oscillateurs émettant les rayons X secondaires. Comment Compton a-t-il déterminé la vitesse v? En appliquant la conservation d'énergie, c'est-à-dire en écrivant
, où v est la vitesse des électrons-oscillateurs émettant les rayons X secondaires. Comment Compton a-t-il déterminé la vitesse v? En appliquant la conservation d'énergie, c'est-à-dire en écrivant 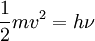 , ce qui conduit à l'expression :
, ce qui conduit à l'expression :
(avec 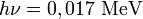 et
et 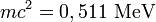 ).
).
Complexe de souhaiter un meilleur accord entre la théorie et la mesure expérimentale de λ / λ'. Ceci est un très bel exemple historique d'une théorie fausse confirmée par des résultats expérimentaux douteux. Quand en octobre 1922 Compton publie un article pour le Conseil National de la recherche, il se rend compte qu'il avait mal lu ses résultats expérimentaux. Il réalise que le décalage en longueur d'onde entre le rayonnement primaire et le rayonnement secondaire n'était pas de 35%, mais uniquement de quelques pourcents : en réalité λ / λ'= 0, 708 / 0, 730 = 0, 969, et non 0, 75. Une fois toujours Compton interprète cela avec sa théorie du rayonnement de fluorescence associé à un effet Doppler, mais désormais en considérant que la vitesse des électrons-oscillateurs était déterminée par la conservation de l'impulsion. En utilisant l'expression 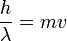 , il arriva à :
, il arriva à :
Cette fois, c'est un bel exemple d'une théorie fausse mais confirmée par des données expérimentales correctes. Dans le mois qui suit, Compton mit tous ces résultats ensemble, utilise ensemble la conservation de l'énergie et la conservation de la quantité de mouvement, utilise l'expression relativiste exacte pour la masse de l'électron et en déduit la désormais célèbre formule du décalage en longueur d'onde apparaissant lors d'une diffusion de rayons X :
À un angle de 90°, le décalage obtenu serait ainsi de 0, 024 Å, ce qu'il compare avec son résultat expérimental (correctement lu) de l'ordre de 0, 022 Å. Il n'y avait plus aucun besoin d'invoquer un rayonnement de fluorescence associé à un effet Doppler. Pour expliquer le changement de longueur d'onde observé, il suffisait de considérer qu'un quantum de lumière d'énergie hν et d'impulsion 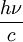 entrait en collision avec un électron libre à la manière d'une boule de billard et le projetait vers l'avant avec une vitesse relativiste.
entrait en collision avec un électron libre à la manière d'une boule de billard et le projetait vers l'avant avec une vitesse relativiste.
Compton expliqua son nouveau calcul dans un premier temps à ses étudiants de l'université Washington en novembre 1922, puis lors d'une rencontre de l'American Physical Society à Chicago le 2 décembre 1922. Il soumit sa théorie quantique de la diffusion à la Physical Review le 10 décembre 1922 ; cet article parut en mai 1923. Arthur Holly Compton avait découvert l'effet Compton.
Démonstration
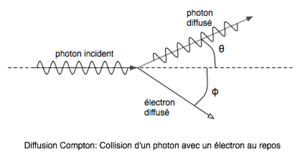
Considérons un photon venant de la gauche et se dirigeant vers la droite avec une impulsion 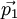 et une énergie E = p1c. Le photon est diffusé par un électron au repos d'énergie d'origine mec2. Le photon est diffusé dans une direction faisant un angle θ comparé à la direction d'origine. L'électron prenant une direction φ, l'impulsion du photon après diffusion sera
et une énergie E = p1c. Le photon est diffusé par un électron au repos d'énergie d'origine mec2. Le photon est diffusé dans une direction faisant un angle θ comparé à la direction d'origine. L'électron prenant une direction φ, l'impulsion du photon après diffusion sera 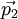 et celle de l'électron
et celle de l'électron 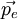 .
.
Variation de la longueur d'onde du photon incident
Pour connaître la variation de longueur d'onde du photon dû à la collision, on utilise la conservation de la quantité de mouvement et la conservation de l'énergie. La première s'écrit, selon les directions «x» et «y», respectivement le long de la trajectoire incidente du photon, et sa perpendiculaire (voir la figure) :
En isolant le terme contenant pe dans les deux équations, en élevant ensuite au carré, puis en additionnant les deux équations, et finalement en utilisant l'identité trigonométrique : cos2φ + sin2φ = 1, on obtient :
D'un autre côté, la conservation de l'énergie s'écrit :
où me et c sont la masse de l'électron, et la vitesse de la lumière respectivement. Le signe γ est utilisé ici comme généralement pour désigner le photon-lui-même. De nouveau en isolant le terme en 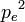 , on obtient :
, on obtient :
En soustrayant les deux expressions obtenues pour 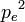 , on peut calculer l'expression :
, on peut calculer l'expression :
On introduit alors l'hypothèse quantique selon laquelle l'impulsion d'un photon est reliée à sa longueur d'onde λ comme : p = h / λ où h est la constante de Planck. Ainsi, l'équation précédente donne directement la variation de longueur d'onde du photon :
De la même manière, en utilisant 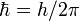 , et l'identité trigonométrique
, et l'identité trigonométrique 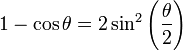 , on peut écrire :
, on peut écrire :
Cette expression est semblable à celle qui s'obtient par un calcul utilisant la mécanique quantique, et les diagrammes de Feynman.
Le facteur : 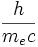 porte le nom de "longueur d'onde de Compton". On le note λC, il vaut 0, 024 Å.
porte le nom de "longueur d'onde de Compton". On le note λC, il vaut 0, 024 Å.
Variation de l'énergie du photon diffusé
La variation de longueur d'onde va de paire avec une variation d'énergie : ΔE donnée par le Postulat de Planck-Einstein : 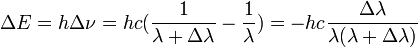 .
.
Ainsi, si un photon incident possède une énergie : E0, alors l'énergie de ce photon après diffusion sur un électron de la matière aura l'énergie :
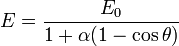
où 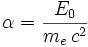 et
et 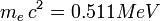 .
.
L'énergie perdue par le photon est entièrement distribuée à l'électron sur lequel la diffusion s'est faite, l'électron prend ainsi l'énergie cinétique :
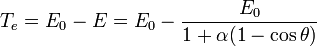
Nous obtenons ainsi la relation suivante :
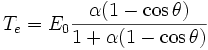
Distribution angulaire de la diffusion Compton
La diffusion Compton n'est pas isotrope, autrement dit que la probabilité pour un photon d'être diffusé vers un certain angle solide dΩ n'est pas constante : en effet, quoique la probabilité de diffusion vers n'importe quel azimut χ est constante, la probabilité de diffusion vers l'angle polaire θ est plus grande lorsque θ est proche de 0, autrement dit que le photon a plus de chance d'être diffusé vers l'avant.
La probabilité pour un photon d'énergie E0 d'être diffusé vers un angle θ quelconque est donnée par la formule de Klein-Nishina :
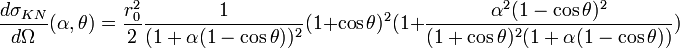
où r0 est le rayon classique d'un électron (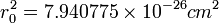 ), et
), et 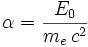 .
.
Une autre forme plus facile à retenir de cette formule fait intervenir le rapport des énergies du photon avant et après collision :
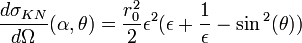
où 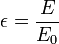
Ainsi la probabilité pour un photon d'énergie E0 de subir une diffusion Compton s'écrit :
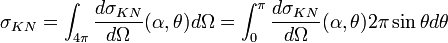
Ce qui s'intègre en :
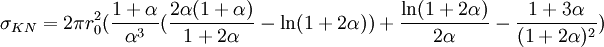
À partir de la formule de Klein-Nishina, il est aussi envisageable de calculer la probabilité qu'un photon diffusé le soit entre deux angles : θ1 et θ2. Calculons pour cela la probabilité de diffusion entre les angles polaires 0 et θ :
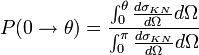
Ce qui s'intègre en :
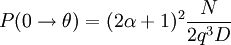
avec :
- q = 1 + α (1 − cosθ)
- N = 2q4 + αq3 (α + 4) + 2q3 (α2 − 2α − 2) lnq − 2q2 (2α + 1) − qα2
- D = 4α (α + 1) 2 (2α + 1) + (2α + 1) 2 (α2 − 2α − 2) ln (2α + 1) − 2α3 (3α + 1)
La probabilité 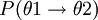 de diffusion entre les angles θ1 et θ2, tels que θ2 > θ1 s'écrit alors :
de diffusion entre les angles θ1 et θ2, tels que θ2 > θ1 s'écrit alors :
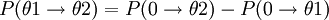
Détection des photons diffusés
Supposons qu'un flux Φ de photons d'énergie E0 frappe un petit échantillon de matière contenant Ne électrons. Supposons à présent qu'on veuille détecter les photons diffusés sur les électrons de cet échantillon avec un détecteur sphérique parfait dont l'angle solide apparent, vu de la source est ΔΩdet
Le nombre de photons par seconde détecté par le détecteur est :
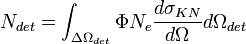
Si qui plus est le détecteur est assez éloigné de l'échantillon de matière (c'est-à-dire πa2 < < R2, où a est le rayon du détecteur et R sa distance à l'échantillon), on considère généralement que le détecteur se trouve à l'angle polaire θ et que 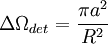 .
.
Il détectera alors le nombre de photons par seconde suivant :
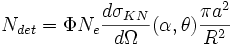
et l'ensemble des photons détectés auront une énergie identique à (ou particulièrement proche de ) :
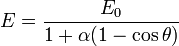
Relation entre l'angle θ de diffusion du photon et l'angle φ d'éjection de l'électron
Supposons que, dans le référentiel du laboratoire, le photon soit diffusé vers un angle θ, alors l'angle d'éjection de l'électron, φ, est donné par la relation suivante :
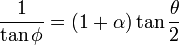
Ainsi si :
- θ = π, alors φ = 0. Cela est facile à comprendre par ressemblance avec le billard : quand la boule blanche (photon) tape directement dans une autre boule (électron) de manière à ce que la blanche revienne en arrière (θ = π), alors l'autre boule va le plus souvent vers l'avant (φ = 0)
- θ = 0, alors
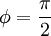 . Ce cas est plus complexe à comprendre mais peut aussi être expliqué par une ressemblance avec le billard. Quand qu'on fait taper la boule blanche (photon) dans une autre boule (électron) de manière à ce que la blanche ne change presque pas de direction et continue tout droit (θ = 0), alors la boule blanche n'a fait qu'effleurer l'autre boule qui est déplacée perpendiculairement à la trajectoire de la blanche (
. Ce cas est plus complexe à comprendre mais peut aussi être expliqué par une ressemblance avec le billard. Quand qu'on fait taper la boule blanche (photon) dans une autre boule (électron) de manière à ce que la blanche ne change presque pas de direction et continue tout droit (θ = 0), alors la boule blanche n'a fait qu'effleurer l'autre boule qui est déplacée perpendiculairement à la trajectoire de la blanche (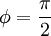 )
)
Régimes Thomson et Klein-Nishina
Selon que le photon incident a une très grande énergie ou pas, on distingue deux «régimes» de la diffusion Compton : les régimes dits «Thomson» (qui donne la diffusion Thomson) et «Klein-Nishina». Par commodité, définissons l'énergie en unités naturelles, c'est-à-dire en unités de l'énergie au repos de l'électron :
où me et c sont la masse de l'électron et la vitesse de la lumière, et le dénominateur n'est rien d'autre que le fameux E=mc2. On peut par conséquent réécrire la variation de longueur d'onde ci-dessus en variation d'énergie comme suit :
Pour des photons avec une très faible énergie, c'est-à-dire avec une énergie énormément plus faible que l'énergie au repos de l'électron (511 keV), on a bien entendu Σ < < 1, et donc :
Ce qui veut dire que si le photon a une très faible énergie face à l'électron au repos, sa longueur d'onde ne changera presque pas. Seule sa direction va changer. C'est ce qu'on nomme le régime Thomson. Dans ce cas, la diffusion Compton retombe sur le cas spécifique de la diffusion Thomson.
Dans le cas opposé où le photon a une grande énergie face à l'électron au repos, Σ > > 1, on obtient alors :
et donc :
où le terme O (1) veut dire «de l'ordre de 1». Dans ce cas, le photon incident a une très grande énergie, mais après la collision, il n'a principalement que l'énergie d'un électron au repos (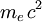 ). Il a par conséquent perdu une grande partie de son énergie. On parle alors de perte «catastrophique», et ce régime est nommé «régime de Klein-Nishina». Remarque : l'effet Compton n'est évidemment pas limité au couple photon-électron. Toute particule chargée électriquement est susceptible d'y être soumise ; cependant, l'effet est plus spectaculaire pour l'électron, la variation de longueur d'onde étant inversement proportionnelle à la masse de la particule (l'électron est la plus légère des particules chargées de l'Univers «ordinaire»).
). Il a par conséquent perdu une grande partie de son énergie. On parle alors de perte «catastrophique», et ce régime est nommé «régime de Klein-Nishina». Remarque : l'effet Compton n'est évidemment pas limité au couple photon-électron. Toute particule chargée électriquement est susceptible d'y être soumise ; cependant, l'effet est plus spectaculaire pour l'électron, la variation de longueur d'onde étant inversement proportionnelle à la masse de la particule (l'électron est la plus légère des particules chargées de l'Univers «ordinaire»).
Diffusion Compton inverse
La diffusion Compton inverse est la diffusion d'électrons sur des photons, leur transférant ainsi une grande partie de leur énergie. C'est un effet particulièrement important en astrophysique, et permet d'expliquer l'effet Sunyæv-Zel'dovich, en cosmologie.
Au niveau théorique la description de l'effet Compton inverse est comparable à celle explicitée plus haut. Il s'agit tout simplement d'un changement de repère. En se plaçant dans le référentiel propre de l'électron après la diffusion on s'aperçoit tandis que la fréquence du photon est augmentée, aux dépens de l'énergie de l'électron incident. Ainsi la différence entre l'effet direct et l'effet inverse gît plutôt dans les conditions initiales : le premier se manifeste lors de la diffusion de photons sur des électrons quasiment au repos (dans la matière), le second dans le freinage d'électrons rapides par des photons qui plus est ou moins basse énergie, présents dans le milieu interstellaire.
Références
- (en) A Quantum Theory of the Scattering of X-Rays by Light Elements. L'article original datant de 1923, publié dans la Physical Review par Arthur H. Compton, sur le site de l'American Institute of Physics.
- (en) Compton Effect [pdf], Michæl Brandl pour Project PHYSNET.
Recherche sur Google Images : |
|
"La diffusion Compton concerne donc ..." L'image ci-contre est extraite du site ead.univ-angers.fr Il est possible que cette image soit réduite par rapport à l'originale. Elle est peut-être protégée par des droits d'auteur. Voir l'image en taille réelle (453 x 403 - 43 ko - jpg)Refaire la recherche sur Google Images |
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.
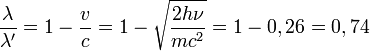
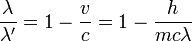
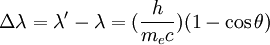
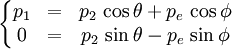
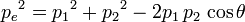
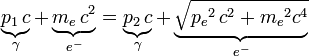
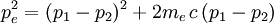
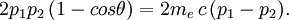
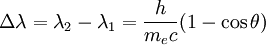
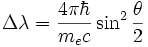
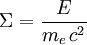
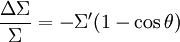
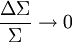
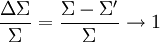
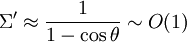

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité