Symétrie conforme

En physique théorique, la symétrie conforme sert à désigner la symétrie sous changement d'échelle, on dit aussi sous dilatation, mais aussi sous les transformations conformes spéciales.

Catégories :

Physique théorique - Théorie conforme des champs - Théorie quantique des champs - Physique quantique - Symétrie

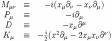
Source image : fr.wikipedia.org
Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur.

Page(s) en rapport avec ce sujet :

Par la suite je me suis dit que puisque la symétrie conforme est une symétrie continue locale, ... en relation avec le (semi) groupe de renormalisation tout ça... (source : forums.futura-sciences)

En physique théorique, la symétrie conforme sert à désigner la symétrie sous changement d'échelle, on dit aussi sous dilatation, mais aussi sous les transformations conformes spéciales. Sa combinaison avec le groupe de Poincaré donne le groupe de symétrie conforme ou plus simplement, groupe conforme.

Voici un exemple de représentation du groupe conforme dans l'espace-temps, ou plus exactement de son algèbre de Lie

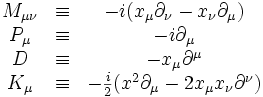
$\begin{matrix} M_{\mu\nu}&\equiv &-i(x_\mu\partial_\nu-x_\nu\partial_\mu)\\ P_\mu&\equiv & -i\partial_\mu \\ D&\equiv &-x_\mu\partialˆ\mu \\ K_\mu&\equiv &-{i\over2}(xˆ2\partial_\mu-2x_\mu x_\nu\partialˆ\nu)\\ \end{matrix}\,$

où les 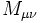$M_{\mu\nu}\,$ sont les générateurs associés au groupe de Lorentz, les 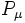$P_\mu\,$ générent les translations de l'espace-temps (les valeurs propres de ces derniers correspondant au quadrivecteur impulsion-énergie), 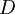$D\,$ génère la transformation par dilatation et enfin les 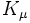$K_\mu\,$ génèrent les transformations conformes spéciales.

Les relations de commutation entre ces générateurs, supplémentaires à celles du groupe de Poincaré sont

$[D,D]=0\,$ , $[D,K_\mu]=-K_\mu \,$

$[D,P_\mu]=P_\mu\,$ , $[K_\mu,K_\nu]=0\,$

$[K_\mu,P_\nu]=\eta_{\mu\nu}D-iM{\mu\nu}\,$

D'autre part, 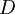$D\,$ est un scalaire de Lorentz et 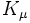$K_\mu\,$ est un vecteur covariant sous les transformations de Lorentz.

Si on considère un espace-temps bidimensionel alors les transformations du groupe conforme sont nommées transformations conformes et dans ce cas particulièrement spécifique le groupe conforme devient de dimension illimitée.

Usages en physique

On voit la naissance de l'invariance conforme dans les phénomènes de turbulence en deux dimensions avec un grand nombre de Reynolds.

Il existe une conjecture affirmant que toute théorie quantique des champs qui est en plus invariante d'échelle admet le groupe conforme complet comme groupe de symétrie globale. Une application spécifique de cette conjecture est donnée dans l'étude des phénomènes critiques (transition de phase du second ordre) dans des dispositifs possédant des interactions locales. Les fluctuations de tels dispositifs sont invariantes conforme au point critique et peuvent par conséquent être décrites par une théorie conforme des champs.

Le plus grand groupe de symétrie global envisageable d'une théorie quantique des champs non-supersymétrique possédant des interactions est un produit direct du groupe conforme avec un groupe interne de symétrie.

En physique des hautes énergies plusieurs théories possèdent la symétrie conforme

La théorie de Yang-Mills supersymétrique N=4.
La théorie des champs vivant sur la surface d'univers des cordes dans le cadre de la théorie des cordes.

Voir aussi

Algèbre superconforme
Théorème de Coleman-Mandula
Invariance d'échelle
Groupe de renormalisation

Recherche sur Amazone (livres) :

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Sym%C3%A9trie_conforme.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.