Quadri-moment
En relativité restreinte, le quadri-moment est une généralisation du moment tridimensionnel classique à un espace-temps à 4 dimensions.
Recherche sur Google Images :

Source image : www.ilnegoziodiangela.com Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Chapitre III : Les différentes particules les plus usuelles..... un propagateur identique à où m est la masse du boson est q le quadri - moment énergie transféré.... (source : physique.quantique.free)
En relativité restreinte, le quadri-moment est une généralisation du moment tridimensionnel classique à un espace-temps à 4 dimensions. Le moment est un vecteur de l'espace (donc le plus souvent à 3 dimensions) ; de la même manière, le quadri-moment est un quadrivecteur de l'espace-temps. Le quadri-moment covariant d'une particule avec un moment tridimensionnel 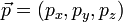 et d'énergie E est
et d'énergie E est
Le quadri-moment est fréquemment utilisé en calcul relativiste car c'est un vecteur de Lorentz. Cela sert à lui appliquer (assez) aisément des Transformations de Lorentz.
Norme de Minkowski : p2
En calculant la norme de Minkowski d'un quadri-moment, on obtient un invariant de Lorentz identique (à un facteur identique à la vitesse de la lumière c près) au carré de la masse au repos de la particule :
en utilisant la convention du dispositif mondial d'unités :
qui est l'inverse du tenseur métrique[1] en relativité restreinte. Puisque 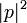 est un invariant de Lorentz, sa valeur reste inchangée par transformations de Lorentz, c'est-à-dire par plongement dans différents référentiels.
est un invariant de Lorentz, sa valeur reste inchangée par transformations de Lorentz, c'est-à-dire par plongement dans différents référentiels.
Relation avec la quadrivitesse
Pour une particule pourvue de masse, le quadri-moment est donné par la masse au repos fois la quadrivitesse :
où la quadrivitesse est
et 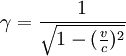 est le facteur de Lorentz et c est la vitesse de la lumière.
est le facteur de Lorentz et c est la vitesse de la lumière.
Conservation du quadri-moment
La conservation du quadri-moment dans un référentiel donné[2] implique deux lois de conservations pour des quantité dites classiques :
- La quantité totale d'énergie E = - p0 est invariante.
- Le moment classique tridimensionnel
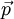 reste invariant.
reste invariant.
On notera au passage que la masse d'un dispositif de particules peut être supérieure à la somme des masses des particules au repos, à cause de l'énergie cinétique. A titre d'exemple, prenons 2 particules de quadri-moment {-5 Gev, 4 Gev/c, 0, 0} et {-5 Gev, -4 Gev/c, 0, 0} ayant chacune une masse au repos de 3 Gev/c2 mais leur masse totale (soit toujours la masse du dispositif) est de 10 Gev/c2. Si ces 2 particules entrent en collision et fusionnent, la masse de l'objet ainsi constitué est de 10 Gev/c2.
Une applicaton pratique en physique des particules de la conservation de la masse au repos permet, à partir des quadri-moments pA et pB de 2 particules créées par la désintégration d'une particule plus grosse ayant un quadri-moment q, de retrouver la masse de la particule d'origine. La conservation du quadrimoment donne qμ = pAμ + pBμ, et la masse M de la particule d'origine est donnée par -|q|2 = M2c2. En mesurant l'énergie et les 3-moments des particules résultantes, on peut calculer la masse au repos du dispositif des 2 particules qui est identique à M. Cette technique est surtout utilisée dans les recherches expériementales sur le boson Z dans les accélérateur de particules.
Si la masse d'un objet ne change pas, le produit scalaire de Minkowski de son quadri-moment et de la quadri-accélération correspondante Aμ est nul. L'accélération est proportionnelle à la dérivée temporelle du moment divisée par la masse de la particule :
Moment canonique en présence d'un champ électromagnétique
Il est aussi utile de définir un moment "canonique" (à 4 dimensions), pour des applications en mécanique quantique relativiste : Pμ, qui est la somme du quadri-moment et du produit de la charge électrique avec le potentiel (qui est un vecteur à 4 dimensions) :
où le 4-vecteur potentiel est une combinaison entre le potentiel scalaire et le potentiel vecteur du champ magnétique :
Voir aussi
Notes
- ↑ Le tenseur métrique est en fait défini à un signe près. On trouvera dans certains ouvrages la convention ημν = (+, −, −, −) au lieu de la convention ημν = (−, +, +, +) adoptée dans cet article. Les résultats physiques sont bien entendu les mêmes quelle que soit la convention choisie, mais il faut prendre garde de ne pas les mélanger.
- ↑ La conservation du quadri-moment veut dire que dans un référentiel donné, le quadri-moment total pν d'un dispositif isolé est conservé. Quand on change de référentiel, le quadri-moment subit une transformation de Lorentz :
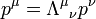 . Le nouveau quadri-moment pμ est à son tour conservé dans ce nouveau référentiel, mais n'est pas identique à pν.
. Le nouveau quadri-moment pμ est à son tour conservé dans ce nouveau référentiel, mais n'est pas identique à pν.
References
- Rindler, Wolfgang (1991). Introduction to Special Relativity (2nd) . Oxford : Oxford University Press. ISBN 0-19-853952-5.
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

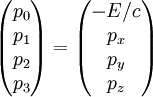
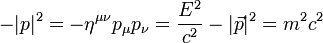
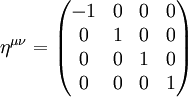
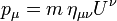
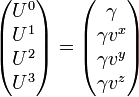
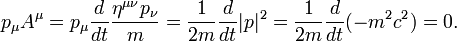
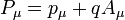
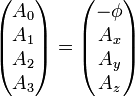

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité