Hamiltonien de Heisenberg

Dans la théorie du magnétisme quantique, l'Hamiltonien de Heisenberg décrit un ensemble de moments magnétiques situés en interaction.

Catégories :

Physique de la matière condensée - Physique quantique

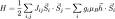
Source image : fr.wikipedia.org
Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur.

Page(s) en rapport avec ce sujet :

Nous avons étudié les interactions magnétiques entre sites de spin S=1 et ... pour un grand nombre ou un nombre illimité de sites, du Hamiltonien modéle... (source : books.google)

Dans la théorie du magnétisme quantique, l'Hamiltonien de Heisenberg décrit un ensemble de moments magnétiques situés en interaction. Cet Hamiltonien s'écrit : 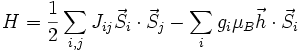$H=\frac 1 2 \sum_{i,j} J_{ij} \vec{S}_i \cdot \vec{S}_j - \sum_i g_i \mu_B \vec{h}\cdot \vec{S}_i$ où $μ B$ est le magnéton de Bohr, $g i$ est le rapport gyromagnétique du $i$ -éme moment situé, 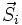$\vec{S}_i$ est un opérateur de spin, 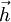$\vec{h}$ est le champ magnétique externe, et $J i j$ est la constante d'échange. Pour $J i j > 0$ l'interaction est antiferromagnétique et pour $J i j < 0$ elle est ferromagnétique. Généralement, les sites $i$ sont positionnés sur les nœuds d'un réseau régulier. Une exception est le cas des verres de spin où les moments magnétiques sont des impuretés magnétiques diluées dans un métal non-magnétique (par exemple du fer dilué dans de l'or ou du manganèse dans du cuivre).

Dans un dispositif sur un réseau bipartite constitué de deux sous-réseaux A et B, si les spins 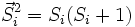$\vec{S}_iˆ2=S_i(S_i+1)$ n'ont pas tous des $S i$ semblables, par exemple si sur le sous-réseau A 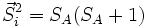$\vec{S}_iˆ2=S_A(S_A+1)$ et sur le sous-réseau B 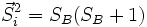$\vec{S}_iˆ2=S_B(S_B+1)$ on parlera d'un modèle ferrimagnétique.

Un concept important dans l'analyse du modèle de Heisenberg est celui de frustration. On dit qu'il y a frustration quand il n'est pas envisageable de minimiser indépendamment chaque terme 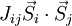$J_{ij} \vec{S}_i\cdot \vec{S}_j$ . Ce cas peut se présenter soit dans les verres de spin, soit dans des modèles antiferromagnétiques sur le réseau triangulaire ou le réseau Kagomé. Dans ce dernier cas on parle de frustration déterministe.

Cas des isolants

Dans un isolant, l'interaction d'échange décroît exponentiellement avec la distance entre les spins situés car elle dépend du recouvrement des orbitales. On peut par conséquent se restreindre à des interactions seulement entre les spins premiers voisins ou entre premier et second voisins. Généralement, l'interaction est due à un mécanisme de superéchange. Elle est le plus fréquemment antiferromagnétique. Les règles de Goodenough permettent de prédire le signe des interactions de superéchange dans les oxydes. Si les liaisons entre les ions magnétiques et les ions oxygène font des angles d'environ 180°, l'interaction d'échange entre les ions magnétiques sera antiferromagnétique. Si les angles sont de 90°, les interactions seront ferromagnétiques.

Cas des verres de spin

Pour des impuretés diluées dans un métal (le cas des verres de spin), l'interaction $J i j$ est une interaction de Ruddermann-Kittel-Kasuya-Yosida médiée par les électrons de conduction qui décroît avec la distance $r i j$ entre les impuretés comme 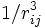$1/r_{ij}ˆ3$ et son signe alterne. Il en résulte surtout que dans un verre de spin, les moments magnétiques n'ont aucune configuration qui minimise l'ensemble des énergies d'échange existantes entre ces moments magnétiques. On parle de frustration. Pour décrire ces interactions aléatoires entre les moments magnétiques, on considère des modèles simplifiés où les ions magnétiques sont positionnés sur un réseau régulier mais les énergies d'échanges sont aléatoires. Quand les interactions aléatoires sont seulement entre premiers voisins on parle d'un modèle d'Edwards-Anderson. Quand les interactions aléatoires sont de portée illimitée, on parle d'un modèle de Sherrington-Kirkpatrick.

Anisotropies

Dans un cristal, la symétrie est réduite à un groupe d'espace. Par conséquent, les interactions entre les spins ne possèdent pas nécessairement l'invariance par le groupe SU (2). Pour pouvoir décrire correctement les propriétés magnétiques, il devient indispensable d'utiliser une généralisation du modèle de Heisenberg contenant des termes d'anisotropie.

Single ion

Dans le cas où les spins 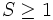$S\ge 1$ , les termes 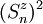$(S_nˆz)ˆ2$ ne se diminuent pas à des constantes. Dans un cristal de symétrie suffisamment basse, il peut par conséquent exister dans le Hamiltonien magnétique des termes de la forme : 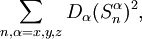$\sum_{n,\alpha=x,y,z} D_\alpha (S_nˆ\alpha)ˆ2,$ où on peut supposer que

∑	D_α = 0
α

, puisque 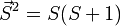$\vec{S}ˆ2=S(S+1)$ . Ces termes sont nommés "single-ion anisotropy". Si $D α > 0$ , ils tendent à empêcher l'aimantation de s'aligner sur la direction $α$ .

Échange anisotrope

Il est aussi envisageable de rencontrer des interactions de la forme : 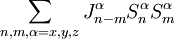$\sum_{n,m,\alpha=x,y,z} J_{n-m}ˆ\alpha S_nˆ\alpha S_mˆ\alpha$

Dans le cas le plus général, ce modèle est nommé modèle XYZ. Dans le cas où 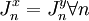$Jˆx_{n}=Jˆy_{n} \forall n$ , et il existe au moins une valeur de $n$ pour laquelle 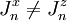$J_nˆx\ne J_nˆz$ , on parle de modèle XXZ (les directions X et Y étant équivalentes). Quand 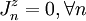$J_nˆz=0, \forall n$ , on parle de modèle XY. Si qui plus est , 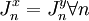$Jˆx_{n}=Jˆy_{n} \forall n$ , on parle de modèle XX ou XX0. Dans le cas où l'interaction est limitée aux premiers voisins, si $| J z | > | J x |, | J y |$ , le dispositif aura tendance à s'aimanter selon la direction z qui est nommée l'axe facile. Dans le cas XXZ, avec $J x > J z$ , le dispositif s'aimante plutôt dans le plan XY qui est nommé plan facile.

En 1956, Matsubara et Matsuda ont montré que dans le cas d'un spin 1/2, le modèle XXZ est équivalent à un modèle de bosons sur réseau avec répulsion de cœur dur et interaction à deux corps mesurée par 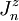$J_nˆz$ . La naissance d'une aimantation dans le plan dans le modèle XXZ équivaut à la condensation de Bose (ou superfluidité des bosons) alors que la naissance d'une aimantation alternée dans le modèle magnétique correspond à un ordre de charge des bosons.

Dzialoshinskii-Moriya

Quand il existe une interaction spin-orbite, il est envisageable de trouver un Hamiltonien magnétique contenant des termes de la forme : 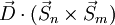$\vec{D}\cdot(\vec{S}_n \times \vec{S}_m)$ , nommés termes de Dzialoshinskii-Moriya. La présence de ces termes tend à imposer un angle entre les moments magnétiques différent de zéro ou cent-quatre-vingt degrés. Surtout, elle donne lieu dans un milieu antiferromagnétique au ferromagnétisme faible.

Kaplan, Shektman, Entin-Wohlmann et Aharony ont montré que si les interaction entre électrons possèdent la symétrie SU (2), cette symétrie étant préservée dans le Hamiltonien magnétique, il existe aussi obligatoirement un terme d'anisotropie supplémentaire dans le Hamiltonien, de la forme 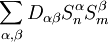$\sum_{\alpha,\beta} D_{\alpha \beta} S_nˆ\alpha S_mˆ\beta$ , où $D αβ$ est un tenseur de rang 2 symétrique.

Échange cyclique

Dans le cas de $3 H e$ solide, il est envisageable d'avoir des échanges à trois ou quatre particules. On doit alors généraliser l'Hamiltonien de Heisenberg en ajoutant des termes d'échange cyclique faisant intervenir respectivement trois ou quatre spins.

Références

Lev Landau et Evguéni Lifchitz, Physique théorique, tome 8 : Électrodynamique des milieux continus, éd. MIR, Moscou [détail des éditions]

Lev Landau et Evguéni Lifchitz, Physique théorique, tome 9 : Physique statistique (II) , éd. MIR, Moscou [détail des éditions]

L. P. Lévy Magnétisme et supraconductuvité (EDP Sciences)
P. W. Anderson Basic Notions of Condensed Matter Physics (Addison-Wesley)
K. Fischer et J. A. Hertz Spin Glasses (Cambridge University Press)
J. M. Ziman Principles of the Theory of Solids (Cambridge University Press)
D. C. Mattis Theory of magnetism (Springer)
R. M. White Quantum Theory of Magnetism (Academic Press)

I. E. Dzialoshinskii J. of. Phys. Chem. Solids 4, 241 (1958).
T. Moriya Phys. Rev. 120, 91 (1960).
T. A. Kaplan Zeitschrift fur Physik B 49, 313 (1983).
L. Shekhtman, O. Entin-Wohlman et A. Aharony Phys. Rev. Lett. 69, 836 (1992).

T. Matsubara et H. Matsuda Prog. Theor. Phys. (Kyoto) 16, 416 (1956)
T. Matsubara et H. Matsuda Prog. Theor. Phys. (Kyoto) 16, 569 (1956)

Recherche sur Amazone (livres) :

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Hamiltonien_de_Heisenberg.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.