Bosons esclaves

Le formalisme des bosons esclaves a été introduit dans le contexte de la théorie des fermions fortement corrélés pour prendre en compte les contraintes de non-double occupation.

Catégories :

Physique quantique

Le formalisme des bosons esclaves a été introduit dans le contexte de la théorie des fermions fortement corrélés pour prendre en compte les contraintes de non-double occupation.

Si on considère un modèle (par exemple le modèle t-J) dans lequel il existe une contrainte :

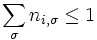$\sum_\sigma n_{i,\sigma}\le 1$ ,

où n_{i, σ} = 0,1 est un nombre d'occupation fermionique, σ = 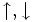$\uparrow,\downarrow$ , la contrainte interdit d'avoir dans l'état i un fermion de spin 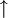$\uparrow$ et un fermion de spin 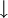$\downarrow$ simultanément, d'où son nom de contrainte de non-double occupation. Pour prendre en compte cette contrainte de façon approchée dans le formalisme de deuxième quantification, il est commode d'élargir l'espace de Hilbert en introduisant des opérateurs de création et d'annihilation pour des bosons fictifs.

Si les opérateurs de création des fermions initiaux sont c ^†_{i, σ}, on introduit les opérateurs de création des bosons et des fermions fictifs par :

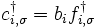
$cˆ\dagger_{i,\sigma}=b_i fˆ\dagger_{i,\sigma}$

et :

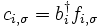
$c_{i,\sigma}=b_iˆ\dagger f_{i,\sigma}$

L'espace des états physiques est défini par la nouvelle contrainte :

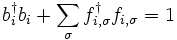
$bˆ\dagger_i b_i +\sum_{\sigma} fˆ\dagger_{i,\sigma} f_{i,\sigma}=1$

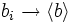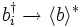Il est dans ce cas possible de traiter le Hamiltonien exprimé en fonction des nouveaux opérateurs par une approximation du champ moyen, en remplaçant $b_i \to \langle b\rangle$ , et $bˆ\dagger_i \to \langle b\rangleˆ*$ . La contrainte permet de fixer 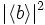$|\langle b\rangle|ˆ2$ en fonction de la densité moyenne des fermions.

Cette approximation de champ moyen est criticable étant donné que elle brise une symétrie de jauge continue, en contradiction avec le théorème d'Elitzur. Cependant, appliquée à la transition métal-isolant, elle donne le même résultat que l'approximation de Gutzwiller.

Cette méthode a été généralisée au modèle de Hubbard en introduisant quatre types différents de bosons esclaves par Kotliar et Ruckenstein. D'autre part, il existe aussi une méthode de fermions esclaves.

Références

N Read and D M Newns J. Phys. C : Solid State Phys. 16 L1055-L1060 (1983).
Piers Coleman Phys. Rev. B 29,3035–3044 (1984).
Gabriel Kotliar and Andrei E. Ruckenstein Phys. Rev. Lett. 57,1362–1365 (1986).

Recherche sur Google Images :

"... bosons et des fermions fictifs ..."
L'image ci-contre est extraite du site fr.wikipedia.org

Il est possible que cette image soit réduite par rapport à l'originale. Elle est peut-être protégée par des droits d'auteur.

Voir l'image en taille réelle (98 x 28 - 1 ko - png)

Refaire la recherche sur Google Images

Recherche sur Amazone (livres) :

Refaire la recherche

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Bosons_esclaves.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 17/11/2008.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.