Longueur d'onde thermique de de Broglie

La longueur d'onde thermique de de Broglie est un concept de la physique statistique et de la mécanique quantique. C'est une grandeur statistique et elle représente la longueur d'onde de De Broglie moyenne des particules d'un gaz porté à une certaine température.

Catégories :

Physique quantique - Physique statistique

La longueur d'onde thermique de de Broglie est un concept de la physique statistique et de la mécanique quantique. C'est une grandeur statistique et elle représente la longueur d'onde de De Broglie moyenne des particules d'un gaz porté à une certaine température. Cette longueur d'onde thermique caractérise l'étalement spatial de la particule associée et le lien entre la mécanique classique et la mécanique quantique.

Particules massives

D'après le principe de la dualité onde-corpuscule, une particule possédant une quantité de mouvement p peut se voit associée une longueur d'onde de $λ = h / p$ , h étant la constante de Planck. Une particule peut être traitée comme une onde avec pour longueur d'onde celle de De Broglie. Pour un gaz porté à une température T, l'énergie typique d'une particule est de l'ordre de $k B T$ , k_B étant la constante de Boltzmann. La relation entre énergie E et quantité de mouvement d'un particule libre non relativiste de masse m étant $E = p 2 / 2 m$ , on peut alors définir la longueur d'onde thermique de De Broglie $λ th$ d'une particule massique en équilibre d'un gaz comme :

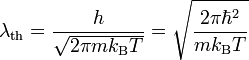$\lambda_{\rm th} =\frac{h}{\sqrt{2\pi m k_\mathrm{B}T}}=\sqrt{\frac{2\pi \hbarˆ2}{m k_\mathrm{B}T}}$ ,

selon qu'on utilise la constante de Planck (h) ou la constante de Planck réduite (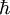 $\hbar$ ).

Le facteur numérique 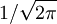$1/\sqrt{2 \pi}$ apparaît a priori arbitraire (il ne correspond pas à la longueur d'onde de De Broglie telle que définie d'ordinaire), et est défini conventionnellement à cette valeur.

Sens physique

La longueur thermique de de Broglie représente un moyen pour déterminer si le dispositif doit être reconnu de manière quantique ou classique. En effet, les effets quantiques commencent à être importants quand la longueur d'onde thermique de de Broglie devient identique avec les autres longueurs caractéristiques du dispositif, comme le libre parcours moyen d'une particule, ou le volume du dispositif. Surtout, sa valeur apparaît dans le calcul explicite où on regarde l'effet des corrections quantiques dans la définition des états d'énergie des particules d'un gaz confinées dans un volume V donné. En mécanique quantique, les énergies envisageables des particules sont quantifiées, tandis qu'en mécanique classique on suppose implicitement que l'ensemble des valeurs d'énergies sont envisageables. La grandeur physique qui importe ici est ce qu'on nomme la fonction de partition, qu'on peut calculer soit dans le cas classique, soit dans le cas quantique. Les calculs indiquent que les deux fonctions de partition changent d'un quantité proportionnelle à

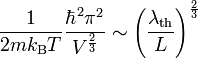$\frac{1}{2 m k_{\rm B} T} \frac{\hbarˆ2 \piˆ2}{Vˆ\frac{2}{3}} \sim \left(\frac{\lambda_{\rm th}}{L}\right)ˆ\frac{2}{3}$ ,

le volume reconnu étant supposé cubique de longueur L.

Voir aussi

Références

(en) Vu-Quoc, L., Configuration integral (statistical mechanics) , 2008.

Recherche sur Google Images :

"? est la longueur d'onde thermique ..."
L'image ci-contre est extraite du site atomoptic.iota.u-psud.fr

Il est possible que cette image soit réduite par rapport à l'originale. Elle est peut-être protégée par des droits d'auteur.

Voir l'image en taille réelle (239 x 155 - 4 ko - gif)

Refaire la recherche sur Google Images

Recherche sur Amazone (livres) :

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Longueur_d%27onde_thermique_de_de_Broglie.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.