Quantification semi-classique

En physique, la quantification semi-classique est une procédure simplifiée servant à quantifier - dans le cadre de la théorie des quanta - un dispositif physique à partir de ses ingrédients classiques, surtout ses trajectoires.

Catégories :

Physique quantique - Physique mathématique

Source image : pagesperso-orange.fr
Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur.

Page(s) en rapport avec ce sujet :

P16 : Dispositifs intégrable : de la mécanique statistique à la théorie quantique.... 2 - Développement semi - classique et interprétation de l'intégrale de chemin.... ou un nouveau système sont conçus à partir de questions ou de ..... quantification de la conductance, mesure à quatre fils, réciprocité, effet Hall... (source : ens-lyon)
... Antenne (En radioélectricité, une antenne est un système servant à rayonner...... Quantification semi - classique Discuter : Quantification semi - classique.... Dispositif intégrable Discuter :Dispositif intégrable ; Dispositif mécanique... (source : techno-science)

En physique, la quantification semi-classique est une procédure simplifiée servant à quantifier - dans le cadre de la théorie des quanta - un dispositif physique à partir de ses ingrédients classiques, surtout ses trajectoires. Michæl Berry utilise à ce propos la formulation imagée : «mettre de la chair quantique sur un squelette classique». Cette procédure simplifiée, qui n'utilise pas l'appareil mathématique complet de la mécanique quantique, est supposée valide dans le régime semi-classique.

La plus ancienne de ces procédures, concernant la quantification de l'atome d'hydrogène, est due à Bohr (1913), donnant lieu au célèbre «modèle de Bohr» à orbites circulaires. Cette procédure fût étendue par Sommerfeld afin d'inclure les orbites elliptiques.

Quantification EBK d'un dispositif intégrable

En 1917, Einstein généralisa à tout dispositif intégrable conservatif la procédure de Bohr-Sommerfeld. La méthode générale d'Einstein fût précisée par Brillouin, puis Keller, donnant lieu à la quantification EBK.

Pour un dispositif intégrable conservatif à N degrés de liberté, il existe en effet N variables d'action qui sont toutes des constantes du mouvement. Ainsi, la dynamique classique d'un dispositif intégrable est elle restreinte à un tore invariant à N dimensions dans l'espace des phases, caractérisé par la valeurs des N actions.

La quantification EBK consiste à n'autoriser que des actions multiples entier (à une constante près) du quantum d'action ; si $C i$ est un contour fermé sur le tore invariant, on pose :

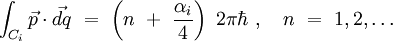
$\int_{C_i} \vec{p} \cdot \vec{dq} \ = \ \left( n \ + \ \frac{\alpha_i}{4} \right) \ 2 \pi \hbar \ , \quad n \ = \ 1, 2, \dots$

Les entiers positifs $α i$ sont des indices de Maslov.

Quantification d'un dispositif non-intégrable

La méthode EBK ne s'applique que pour de dispositifs intégrables. Quand le dispositif n'est pas intégrable, a fortiori quand le dispositif est chaotique, une procédure de quantification semi-classique de l'énergie du dispositif est apportée par la formule des traces de Gutzwiller.

Articles liés

Théorie du chaos
Formule des traces de Gutzwiller
Géométrie spectrale

Vulgarisation

Lorenzo J. Curtis & David G. Ellis ; Use of the Einstein–Brillouin–Keller action quantization, American Journal of Physics 72 (12) (December 2004), 1521-1523.

Ouvrages de référence

Martin C. Gutzwiller ; Chaos in Classical and Quantum Mechanics, Springer-Verlag (1990), ISBN 0-387-97173-4.
V. P. Maslov, Théorie des perturbations et methodes asymptotiques, Dunod (1972).

Articles historiques

Albert Einstein ; Zum Quantensatz von Sommerfeld und Epstein, Verhandlungen der Deutschen Physikalischen Gesellschaft 19 (1917), 82-92. Reproduit dans : The Collected Papers of Albert Einstein, A. Engel translator, Princeton University Press, 6 (1997), 434.
Joseph B. Keller ; Annals of Physics (NY) 4 (1958), 180.
Joseph B. Keller ; Annals of Physics (NY) 9 (1960), 24
Martin C. Gutzwiller ; Journal of Mathematical Physics 12 (1971), 343.

Recherche sur Amazone (livres) :

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Quantification_semi-classique.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.