Relation de dispersion

En physique théorique, une relation de dispersion est une relation entre la pulsation ω et le vecteur d'onde d'une onde monochromatique.

Catégories :

Électromagnétisme - Physique quantique - Mécanique ondulatoire

Source image : www.enseeiht.fr
Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur.

Page(s) en rapport avec ce sujet :

Dès que la longueur d'onde est supérieureà quelques cm, le terme de pesanteur domine; la relation... La relation de dispersion est du type ω = constante. k2... (source : webapps.fundp.ac)
d'onde, q, de I'ordre du dixi6me de la zone de Brillouin, q, , , , , . Dans cette gamme, la relation de ... Quand la relation de dispersion est connue, cette... (source : hal.archives-ouvertes)
dans la limite des grandes longueurs d'onde k = 2 π /λ → 0. Relation de ... La relation de dispersion se compose de 3 branches dites «acoustiques» [ LA, ... (source : cours.phy.ulaval)

En physique théorique, une relation de dispersion est une relation entre la pulsation $ω$ et le vecteur d'onde 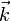$\vec{k}$ d'une onde monochromatique.

Par extension, la dualité onde-corpuscule de la physique quantique conduit à l'introduction de relation de dispersion pour une particule, comme relation entre son énergie $E$ et sa quantité de mouvement 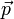$\vec{p}$ .

Onde monochromatique de célérité c dans un milieu non dispersif

Un milieu non dispersif est caractérisé par un indice n indépendant de la pulsation. En notant : 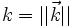$k = || \vec{k} ||$ , la relation de dispersion s'écrit :

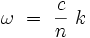$\omega \ = \ \frac{c}{n} \ k$

La vitesse de phase est alors constante :

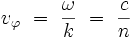$v_{\varphi} \ = \ \frac{\omega}{k} \ = \ \frac{c}{n}$

et est identique à la vitesse de groupe :

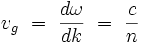$v_{g} \ = \ \frac{d\omega}{dk} \ = \ \frac{c}{n}$

Onde monochromatique de célérité c dans un milieu dispersif

Dans un milieu dispersif, l'indice optique n dépend de la pulsation $ω$ . En notant : 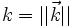$k = || \vec{k} ||$ , la relation de dispersion s'écrit :

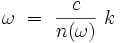$\omega \ = \ \frac{c}{n(\omega)} \ k$

La vitesse de phase dépend alors explicitement de la pulsation :

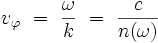$v_{\varphi} \ = \ \frac{\omega}{k} \ = \ \frac{c}{n(\omega)}$

La vitesse de groupe n'est généralement plus identique à la vitesse de phase, mais lui est reliée par la relation de Rayleigh :

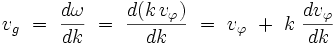$v_{g} \ = \ \frac{d\omega}{dk} \ = \ \frac{d(k \, v_{\varphi})}{dk} \ = \ v_{\varphi} \ + \ k \ \frac{d v_{\varphi}}{dk}$

Particule non relativiste de masse m

En notant : 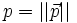$p = || \vec{p} ||$ , la relation de dispersion s'écrit :

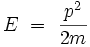$E \ = \ \frac{pˆ2}{2m}$

Particule relativiste de masse nulle

$E \ = \ p \, c$

Notes

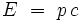Recherche sur Amazone (livres) :

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Relation_de_dispersion.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.