Opérateur de position de Newton-Wigner

En théorie quantique relativiste, l'opérateur de position de Newton-Wigner est un opérateur introduit en 1949 par Newton et Wigner pour tenter de décrire la position de particules massives relativistes de spin arbitraire.

Catégories :

Physique théorique - Physique quantique

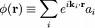
Source image : fr.wikipedia.org
Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur.

Page(s) en rapport avec ce sujet :

Wiki de Théorie quantique des champs. Retrouvez la definition Wikipedia de ... l'opérateur de position de Newton - Wigner apporte des éléments de réponse.... (source : books.google)

En théorie quantique relativiste, l'opérateur de position de Newton-Wigner est un opérateur introduit en 1949 par Newton et Wigner pour tenter de décrire la position de particules massives relativistes de spin arbitraire.

Le problème de la localisation

Dans quelle mesure est-il envisageable de parler de la localisation d'une «particule» quantique dans une région de l'espace (et dans le temps) ?

Dans le cadre de la mécanique quantique non-relativiste, on dispose d'un opérateur position 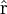$\ \hat{\mathrm{r}} \$ hermitien qui sert à préciser de façon cohérente la notion de localisation d'une particule^[1].

En physique relativiste, les transformations de Lorentz mélangent les coordonnées d'espace et de temps. En mécanique quantique relativiste, si le vecteur position classique était associé à un opérateur position quantique "à la Heisenberg", il devrait aussi exister un opérateur temps. Or, un vieil argument de Pauli suggère^[2] qu'il n'existe pas d'opérateur temps hermitien en mécanique quantique^[3]. La solution usuelle consiste à abandonner a priori la notion d'opérateur position en passant à la théorie quantique des champs définie sur l'espace-temps.

L'opérateur position de Newton-Wigner (1949)

En 1949, Newton et Wigner ont réussi à construire un nouvel «opérateur position» pour les particules massives relativistes de spin arbitraire. Moyennant quelques hypothèses générales raisonnables, ils ont créé un opérateur non-local dans l'espace physique. Les «états situés» associés à cet opérateur ne sont pas des distributions de Dirac. L'état situé autour de l'origine possède à longue distance une décroissance exponentielle avec une échelle caractéristique identique à la longueur d'onde de Compton de la particule massive. De plus, ces états situés ne sont pas invariants par transformation de Lorentz.

La construction de Newton-Wigner couvre aux particules de masse nulle de spin 0 (décrites par l'équation de Klein-Gordon) et de spin 1/2 (décrites par l'équation de Dirac), mais pas au photon, de spin 1.

Bibliographie

T. D. Newton and E. P. Wigner ; Localized States for Elementary Systems, Review of Modern Physics 21 (1949), 400-406. pdf.

Notes

↑ Quand la particule est dans un état 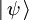, on peut par exemple calculer :
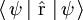- la position moyenne, donnée par : $\langle \, \psi \, | \ \hat{\mathrm{r}} \ | \, \psi \, \rangle$ ;
- l'écart quadratique moyen $Δr$ autour de cette position moyenne (dispersion), défini par :
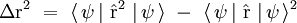
$\Delta \mathrm{r}ˆ2 \ = \ \langle \, \psi \, | \ \hat{\mathrm{r}}ˆ2 \ | \, \psi \, \rangle \ - \ \langle \, \psi \, | \ \hat{\mathrm{r}} \ | \, \psi \, \rangleˆ2$
La particule quantique est d'autant mieux située que cette dispersion est petite. La mécanique quantique n'interdit d'ailleurs pas de la prendre nulle, auquel cas la localisation spatiale est idéalement réalisée. (Il y a alors une dispersion maximale en quantité de mouvement pour satisfaire les inégalités de Heisenberg. )
↑ Un auteur a récemment remis en cause la validité du raisonnement de Pauli ; cf. e. g. : quant-ph/9908033 ; quant-ph/0111061 ; quant-ph/0303106.
↑ En mécanique hamiltonienne, temps et énergie sont conjugués : le hamiltonien est le "générateur illimitétésimal" des translations dans le temps. Par ressemblance avec le couple position/impulsion satisfaisant $[\hat{\mathrm{x}}ˆi, \, \hat{\mathrm{p}}_j ] = i \ \hbar \ \hat{\mathrm{\delta}}_jˆi$ , on serait alors amené à écrire : $[\hat{\mathrm{H}},\hat{\mathrm{t}}] = (\pm) \ i \ \hbar \ \hat{\mathrm{1}}$ . 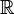Par conséquent, l'opérateur temps deviendrait réciproquement le générateur illimitétésimal des translations en énergie, et le spectre d'énergie serait le continuum $\mathbb R$ entier, ce qui veut dire que l'énergie ne serait plus bornée inférieurement. Or la mécanique quantique a exactement été découverte pour rendre compte de la stabilité des atomes, et surtout de l'existence d'un état essentiel d'énergie finie.

Articles liés

Recherche sur Amazone (livres) :

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Op%C3%A9rateur_de_position_de_Newton-Wigner.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.