Système d'unités du corps noir

Pour une information qui plus est haut niveau, regarder l'article corps noir.

Catégories :

Article à recycler (physique) - Physique quantique - Thermodynamique

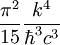
Source image : fr.wikipedia.org
Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur.

Page(s) en rapport avec ce sujet :

Les lois déterminant l'état de la matière dans un corps noir s'appuient sur ... (λ) et la température (T) exprimées dans le Dispositif Mondial d'unités.... (source : astro-rennes)
Le nombre baryonique d'un dispositif se définit comme le nombre de baryons moins le nombre d'antibaryons.... Elle détermine la taille d'unités d'énergie, de longueur ou de masse qui... Le rayonnement du corps noir a été calculé par Max Planck..... Loi de conservation : principe selon lequel la valeur totale d'une... (source : books.google)
Au cours de la montée en température du corps noir, deux phénomènes se... Cette constante qui a pour valeur 2 897 800 (loi de Wien) permet ainsi de calculer, ... D'ailleurs, parmi les 7 unités de base du Dispositif Mondial d'Unités, ... (source : site.voila)

Pour une information qui plus est haut niveau, regarder l'article corps noir.

En physique, le corps noir est un simple four avec une toute petite ouverture. Cette ouverture laisse passer un rayonnement électromagnétique, caractéristique, décrit par Max Planck. Le corps noir peut aussi être décrit comme un gaz de photons à l'équilibre thermodynamique dans une enceinte fermée de température T.

Dans cet article, on ne cherche qu'à montrer comment retenir les deux lois principales (loi de Stefan et loi de Wien)

Chacun connaît l'expression : il fait noir comme dans un four ! Mais au fur et à mesure que la température du four augmente, la lumière qui sort du four augmente en intensité, et vire du rouge au blanc-bleu (et alors, il faut regarder avec un masque anti-UV).

Les deux lois principales sont :

l'intensité fluctue comme Tˆ4, nommée loi de Stefan
le maximum de cette intensité a lieu pour la fréquence, 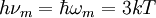$h\nu_m = \hbar \omega_m = 3 kT$ ), nommée loi de Wien du corps noir.

Le dispositif d'unités naturelles construit sur [kT, c, 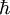$\hbar$ ] sert à retenir facilement ces deux lois. C'est , évidemment, l'intérêt de ces dahus (dimensional analysis of heuristic units system), introduits déjà par Maxwell.

Remarque : Il faut connaître ces lois pour comprendre l'effet de serre. Les retenir est le but de l'article.

Déduction des trois unités élémentaires

masse m telle que mc² = kT (ce qui ne veut pas dire du tout que le photon ait une masse ! Voilà un bel exemple de la limitation des Dahus : ils ne peuvent pas empêcher les gens de dire des bêtises !).

fréquence f telle que h. f = kT

vitesse : c

Les autres unités

On demande fréquemment l'énergie des photons contenue dans le volume V :

$U/V = d.u.[kT,\hbar,c] = \frac{(kT)ˆ4}{\hbarˆ3 cˆ3}$

le résultat exact du calcul, via la loi de Planck est : multiplier par 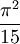$\frac{\piˆ2}{15}$

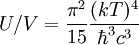$U/V =\frac{\piˆ2}{15} \frac{(kT)ˆ4}{\hbarˆ3 cˆ3}$
Loi exacte de Stefan

Comme pour l'ensemble des corps relativistes en dimension trois, la pression vaut P =1/3 U/V. Par conséquent l'enthalpie H = U + PV vaut 4/3U.

Loi d'émission de Stefan

On demande fréquemment la puissance lumineuse en watts qui sort de la petite ouverure. La réponse est bien entendu que s'il y a deux ouvertures semblables, il sort 2 P. On donne par conséquent la puissance émise par unité de surface. Par analyse dimensionnelle, P/S est U/V. c Le résultat exact est : U/V (c/4).

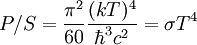$P/S =\frac{\piˆ2}{60} \frac{(kT)ˆ4}{\hbarˆ3 cˆ2}= \sigma Tˆ4$
Loi exacte d'émission de Stefan

Application pour l'effet de serre

Le Soleil est reconnu comme un corps noir émettant P = 4 10ˆ26 Watts par sa surface 4Pi. R² avec R ∼700 000 km : ceci sert à calculer la température de surface du corps noir correspondant, Ts = 5700 K.

Pour n'importe quel corps noir sphérique localisé à d =150 10ˆ6 km, la température d'équilibre sera :

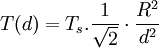
$T(d) = T_s . \frac{1}{\sqrt 2}\cdot \frac{Rˆ2}{dˆ2}$

La Terre ayant un albédo moyen de 0.30, la température est en fait de 255K (soit -18°C).

La Terre reçoit 341-342 W/m² en moyenne (bien entendu l'équateur reçoit plus que les pôles! C'est le rééquilibrage de cette réception différentielle qui crée : les vents, puis les courant marins).

D'autre part, l'effet de serre joue, et la température moyenne de la Terre est 255+33 = 288 K ; soit 33K qui plus est par effet de serre. Ce dernier ne cessant d'augmenter par production de dioxyde de carbone, l'Océan s'évapore plus et le cycle de la pluie se trouve être plus rapide : il neige par conséquent légèrement plus en Antarctique, comme on peut le constater facilement depuis 20 ans (dans les autres parties du monde, cela est vérifié aussi, mais en moyenne seulement : il faut prendre des climats particulièrement stables pour ne pas mélanger trop de variables (Les rapports successifs du GIEC sont exemplaires dans leurs affirmations prudentes) ).

Loi de Wien

Rappel de l'énoncé de la loi de Wien :le rayonnement émis par le four est nul aux basses fréquences ainsi qu'aux hautes fréquences. Il passe par un maximum pour une fréquence f dite fréquence de Wien variant linéairement avec la température absolue T

L'analyse dimensionnelle donne immédiatement h. f = kT.

Le résultat exact donné par la loi de Planck en fréquence est hf = b. kT ; la valeur numérique b est telle que :b = 3 (1-exp (-b) ), soit b = 2.822...

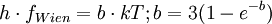$h\cdot f_{Wien} = b \cdot kT ; b=3(1-eˆ{-b})$
Loi exacte du maximum d'émission de Wien

Si on compare avec la courbe de sensibilité des cônes et des bâtonnets de la rétine, on trouve que l'œil humain a subi une "merveilleuse" adaptation à ce créneau du "visible" (pour nous). Les chats ont des habitudes de chasse différentes et par conséquent une autre adaptation. De même, dans l'eau, les animaux rouges se camouflent mieux. L'étude de la vue des rapaces montre aussi une remarquable adaptation.

Remarque : attention, piège classique : on n'obtient pas la même valeur de b en prenant la loi de Planck en longueur d'onde, comme on pourra facilement le vérifier en regardant l'article corps noir. C'est un piège courant en principe des densités de probabilités.

Thermodynamique du corps noir

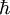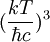Le nombre de photons par unité de volume est d. u. [kT, $\hbar$ , c] = $(\frac{kT}{\hbar c})ˆ3$ .

Pour le calcul exact, multiplier par 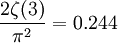$\frac{2\zeta (3)}{\piˆ2}= 0$4$

Ainsi la loi du gaz de photons est remarquable de simplicité :

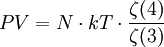$PV = N \cdot kT \cdot \frac{\zeta (4)}{\zeta(3)}$
Équation d'état exacte du gaz de photons

(pour mémoire, on rappelle que la fonction zeta (s) de Riemann vaut 1.2020... pour s= 3 et 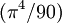$\ (\piˆ4/90)$ pour s = 4).

Si on dilate lentement et réversiblement le volume d'un corps noir, chaque longueur d'onde subit l'effet Doppler, sans qu'il y ait variation du nombre de photons dans chaque mode propre : c'est dire que l'entropie S fluctue comme V. (kT) ˆ3 :

très précisément G = H-TS = 0 pour un corps noir.

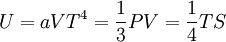$U = aVTˆ4 = \frac{1}{3} PV = \frac{1}{4} TS$
Thermodynamique du corps noir

Application au fond diffus cosmologique

Penzias et Wilson ont reçu le prix Nobel pour avoir détecté ce rayonnement prévu par Gamow. Lors du big-bang, l'univers s'est dilaté et la température a baissé et la formation d'atomes (H+) + (e-) -> H a pu se produire. Il s'est produit alors découplage entre matière neutre et rayonnement.

Depuis, le nombre de photons "fossiles" n'a plus varié.

Le prochain Satellite Planck, qui prendra la suite de COBE (cf Cosmic Background Explorer, et Nobel 2006 :John. C. Mather & George Smoot) et de W_MAP, donnera la température de ce rayonnement avec une précision de 10ˆ (-6) K, ce qui permettra de voir toujours mieux les légères perturbations au moment du "découplage matière-rayonnement" lorsque les premiers atomes se sont constitués. La température actuelle est 2.7283 K environ (cf laboratoire du LERMA, obs de Paris).

Conclusion

En réalité, on a escamoté ici la loi de Planck (cf corps noir) et tout son historique passionnant. Mais on peut précisément par une analyse soigneuse de Dahus montrer comment Planck a réussi à surmonter la contradiction apparente entre la loi de Wien (1896) pour les grandes fréquences et la loi de Jeans-Rayleigh pour les petites : cette subtile analyse est due à Alfred Kastler et mériterait qu'on la publie ici. Superbe aussi est l'analyse de Richard Feynman du <<(n+1)_émis.n(A_excité) pour n_absorbé.n(A_fondamental)>>, qui résume la majeure partie de cette formidable saga scientifique.

L'analyse de la physique en termes simples comme ont su le faire John Archibald Wheeler et Victor Weisskopf et Mr Tompkins (George Gamow), via leurs Dahus, permet ainsi de comprendre énormément avec peu de moyens.

Voir aussi

cours de l'École Polytechnique sur le rayonnement, par exemple (BLANC, CHASSEFIERE, LE TREUT, ... ).

Pour l'analyse dimensionnelle via les dispositifs d'unités corrects (dimensional analysis of heuristic units systems), voir par exemple : cours de l'ENS (Stephan Fauve), ou hydrodynamique de Guyon, ou cours Moffatt (microhydrodynamics), ou LA référence historique : Saint-Guilhem (Eyrolles 1971), et VASCHY : Annales télégraphiques, 1892 où est rédigé le théorème PI de Vaschy-Buckingham. Toutes ces questions d'analyse sont développées dans *SEDOV (analyse dimentionnelle, ed MIR)

Barenblatt (dimensional analysis) qui sont les sources du cours S. FAUVE.

Recherche sur Amazone (livres) :

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Syst%C3%A8me_d%27unit%C3%A9s_du_corps_noir.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.