Logique quantique
La logique quantique est celle qui respecte les postulats de la mécanique quantique. Surtout les observables n'étant pas nécessairement commutatives, le théorème d'Heisenberg, entraîne la notion d'intricats, notion purement quantique : par...
Recherche sur Google Images :
Source image : fr.wikipedia.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- mations unitaires et chaque porte logique quantique est une matrice..... A. R. Calderbank, P. W. Shor : Good quantum error-correcting codes exist, Phys.... (source : smf.emath)
La logique quantique est celle qui respecte les postulats de la mécanique quantique. Surtout les observables n'étant pas nécessairement commutatives, le théorème d'Heisenberg (cf. principe d'incertitude), entraîne la notion d'intricats, notion purement quantique : par exemple la notion de chat mort & vivant, comme dans le célèbre paradoxe du chat de Schrödinger.
Ce que John von Neumann a montré clairement, en réfléchissant aux fondations de la mécanique quantique, est que la logique d'Aristote (cf. Organon) était en contradiction avec la logique quantique. Surtout la notion du tiers exclu n'existe pas en logique quantique.
Mackey, puis Varadarajan ont développé ces réflexions, puis énormément d'autres.
Il a fallu énormément de temps à la communauté scientifique pour sauter le pas et faire abstraction de 2000 ans de logique aristotélicienne; on en veut pour preuve le nombre de décennies nécessaires pour écrire et réécrire sur le "voile soulevé " (d'Espagnat, école des variables cachées, école de BOHM, etc. ).
Néanmoins, les inégalités de Bell (1964) ont montré, par l'expérience (1982) que la réalité de la mécanique quantique était certainement non-locale : une paire intriquée le reste fût-elle grande de 20 km (cf. Paradoxe EPR). On vend aujourd'hui des crypteurs quantiques infalsifiables, à cause de ce comportement de la logique quantique (cf. cryptologie quantique).
De même, le théorème de non-clonage est validé par la mécanique quantique et la réalisation pratique de la téléportation quantique d'information (Haroche, professeur au Collège de France, préfère parler de fax quantique) est devenue une réalité.
Enfin, au moins sur le papier, il est démontré que les intricats permettent de réaliser des calculs plus rapidement en informatique quantique (algorithme de Shor, codes quantiques correcteurs d'erreurs, ... ).
Le théorème de Grünwald & van Hove
Pour montrer la subtilité de la non-commutativité, rappelons ce théorème qui fait obstruction à la quantisation de Hermann Weyl, par conséquent invalidée.
Weyl avait assez judicieusement choisi de passer de la mécanique classique à la mécanique quantique en remplaçant les crochets de Poisson de la géométrie symplectique en commutateur sur les observables.
Soit W (f) := 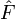 , l'opérateur observable associé à la variable classique f (q, p).
, l'opérateur observable associé à la variable classique f (q, p).
Pour Weyl, on aurait dû avoir [-i. W (f), -i. W (g) ] := -i. W ({f, g}).
où {f, g} sert à désigner le crochet de Poisson.
Et pour obtenir la quantification de q²p² on aurait pris le symétrisé 1/6 (Q²P² + QPQP + QP²Q + PQ²P + PQPQ + P²Q²).
Ce n'est malheureusement pas envisageable !
Considérons par exemple [W (q³), W (p³] et {x³, p³}= 3q². 3p²-0.
Convenons de rejeter l'opérateur Q à droite gràce à QP = PQ +i :
9 W (q²p²) = 9/6 (Q²P² + QPQP + QP²Q + PQ²P + PQPQ + P²Q²) = 3 (3P²Q² +6iPQ -3/2).
Or [Q³, P³]= 9 P²Q² +18 i PQ -6 (après calculs) n'est pas identique à la valeur précédente!
Géométrie non-commutative
Le processus de Weyl n'est pas le bon ! Il faudra pour obtenir la bonne mécanique quantique opérer en géométrie non commutative, c'est-à-dire avec un espace des phases non-commutatif. Or exactement la construction de cette géométrie est liée à la logique quantique, par une voie subtile récemment défrichée par Alain Connes et Pierre Cartier : le groupe sous-tendant l'architecture de la mécanique quantique n'est pas le groupe unitaire, mais une variante affinée. Par conséquent les quantités illimitées qui perturbent énormément les physiciens de la renormalisation deviennent au contraire compréhensibles, et en bonne logique quantique, tout rentre dans le rang.
Voir aussi
Bibliographie
- John von Neumann : mathematical foundations of Q M ; Princeton, 1955.
- Mackey : idem ; Benjamn, 1963.
- Varadarajan : geometry of Q theory. van Nostrand, 1968.
- Kitæv : classical & quantum computation ; AMS47, 2002
- Hirvensalo : Q computing, springerV, 2001
- Alain Connes : non-commutative geometry, springerV1831, 2004
- G. Birkhoff and J. von Neumann, The Logic of Quantum Mechanics, vol 37, 1936.
- D. Cohen, An Introduction to Hilbert Space and Quantum Logic, Springer-Verlag, 1989. This is a thorough but elementary and well-illustrated introduction, suitable for advanced undergraduates.
- D. Finkelstein, Matter, Space and Logic, Boston Studies in the Philosophy of Science vol V, 1969
- A. Gleason, Measures on the Closed Subspaces of a Hilbert Space, Journal of Mathematics and Mechanics, 1957.
- R. Kadison, Isometries of Operator Algebras, Annals of Mathematics, vol 54 pp 325-338, 1951
- G. Ludwig, Mathematical Foundations of Quantum Mechanics, Springer-Verlag, 1983.
- G. Mackey, Mathematical Foundations of Quantum Mechanics, W. A. Benjamin, 1963 (paperback reprint by Dover 2004).
- J. von Neumann, Mathematical Foundations of Quantum Mechanics, Princeton University Press, 1955. Reprinted in paperback form.
- R. Omnès, Understanding Quantum Mechanics, Princeton University Press, 1999. An extraordinarily lucid discussion of some logical and philosophical issues of quantum mechanics, with careful attention to the history of the subject. Also discusses consistent histories.
- C. Piron, Foundations of Quantum Physics, W. A. Benjamin, 1976.
- H. Putnam, Is Logic Empirical, Boston Studies in the Philosophy of Science vol. V, 1969
- Hermann Weyl, The Theory of Groups and Quantum Mechanics, Dover Publications, 1950.
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.


 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité