Téléportation quantique
La téléportation quantique est un protocole de communications quantiques consistant à transférer l'état quantique d'un dispositif vers un autre dispositif identique et scindé spatialement du premier en mettant à profit l'intrication quantique.
Recherche sur Google Images :

Source image : www.futura-sciences.com Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- LA TÉLÉPORTATION QUANTIQUE est un moyen de faire voyager de l'information... c) L'état quantique d'un N- qubit est un vecteur dans un espace analogue à ... (source : www-reynal.ensea)
- quantique»). Dans les autres cas, Bob obtient l'état du qubit d'origine à une..... La Téléportation Quantique est une illustration spectaculaire d'un des ... (source : taoufik.amri.free)
- téléportation quantique alors ? La téléportation quantique est une...... expérience est par conséquent la téléportation de l'état quantique d'un photon sur un autre photon localisé à ..... Long-distance teleportation of qubits at telecommunication... (source : colder)
La téléportation quantique est un protocole de communications quantiques consistant à transférer l'état quantique d'un dispositif vers un autre dispositif identique et scindé spatialement du premier en mettant à profit l'intrication quantique. Au contraire de ce que le nom laisse entendre, il ne s'agit par conséquent pas de transfert de matière. Le terme de téléportation quantique est utilisé pour souligner le fait que le processus est destructif : à l'issue de la téléportation, le premier dispositif ne sera plus dans le même état qu'originellement.
Avant en premier lieuer le protocole lui-même, nous allons préciser un certain nombre de notions élémentaires d'une nouvelle science en train de naître : l'information quantique.
Le qubit : lorsque le bit devient quantique !
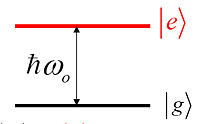
Toute information numérique est encodée sous forme de mots binaires dont l'entité unique et indivisible est le bit (de l'anglais binary digit). Cette variable binaire ne peut prendre que deux états différents «0» et «1» correspondant par exemple à la présence ou non d'un signal électrique, lumineux ou autre. En physique quantique, cette situation se généralise sans difficulté avec un dispositif à deux niveaux : un niveau essentiel 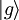 et un niveau excité
et un niveau excité 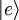 scindé du premier d'une énergie non nulle
scindé du premier d'une énergie non nulle 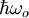 , où ωo est par exemple la fréquence de Bohr d'une certaine transition atomique qu'on sélectionne avec un laser asservi sur cette fréquence. Naturellement, on identifiera l'état binaire «0» à l'état essentiel du dispositif à 2 niveaux et l'état binaire «1» à l'état excité du dispositif qu'on notera désormais par les kets
, où ωo est par exemple la fréquence de Bohr d'une certaine transition atomique qu'on sélectionne avec un laser asservi sur cette fréquence. Naturellement, on identifiera l'état binaire «0» à l'état essentiel du dispositif à 2 niveaux et l'état binaire «1» à l'état excité du dispositif qu'on notera désormais par les kets 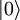 et
et 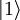 . Ces deux états forment alors la base de l'espace de Hilbert du dispositif, et l'état de ce dernier s'écrira généralement comme
. Ces deux états forment alors la base de l'espace de Hilbert du dispositif, et l'état de ce dernier s'écrira généralement comme 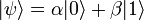 où les paramètres complexes
où les paramètres complexes 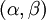 vérifient la condition de normalisation
vérifient la condition de normalisation 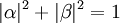 . On nomme alors qubit (pour quantum binary digit) un tel dispositif à deux niveaux utilisé comme brique élémentaire de la logique quantique. Etant donné l'arbitraire de phase d'un état quantique
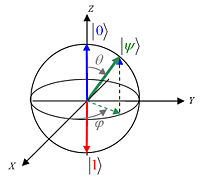
. On nomme alors qubit (pour quantum binary digit) un tel dispositif à deux niveaux utilisé comme brique élémentaire de la logique quantique. Etant donné l'arbitraire de phase d'un état quantique 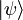 , on peut représenter l'état d'un qubit par un vecteur parcourant la sphère de Bloch avec :
, on peut représenter l'état d'un qubit par un vecteur parcourant la sphère de Bloch avec :
A la différence du bit classique, il est impossible de déterminer (de lire) l'état d'un qubit sans projeter ce dernier sur l'un des états binaires classiques. Alors on peut penser qu'il suffit de multiplier un qubit afin d'en déterminer l'état par mesures répétées sur les copies du qubit d'origine. Cependant, la possibilité d'une telle multiplication des copies du qubit est interdite par la physique quantique, elle fait même l'objet d'un théorème.
Théorème de non clonage quantique
Pour conserver les probabilités, les opérations d'évolution en mécanique quantique sont le plus souvent unitaires, et on peut exiger d'une opération de clonage 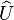 d'un qubit
d'un qubit 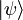 sur un autre qubit
sur un autre qubit 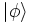 jouant le rôle de support vierge d'être unitaire. Ainsi, cette opération vérifiera pour un certain qubit
jouant le rôle de support vierge d'être unitaire. Ainsi, cette opération vérifiera pour un certain qubit 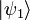 :
:
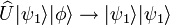 .
.
Or, cette opération ne doit pas dépendre de l'état à cloner et est valable pour un autre état a priori différent du premier :
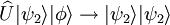 .
.
Le calcul du recouvrement entre ces deux opérations conduit à soit avoir deux états semblables (trivial) 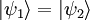 ou des états orthogonaux
ou des états orthogonaux 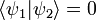 . Finalement, on vérifie qu'on ne peut pas cloner une superposition linéaire de deux états incompatibles, ce qui est précisement le cas d'un qubit. On obtiendrait alors un état intriqué de la forme suivante :
. Finalement, on vérifie qu'on ne peut pas cloner une superposition linéaire de deux états incompatibles, ce qui est précisement le cas d'un qubit. On obtiendrait alors un état intriqué de la forme suivante :
L'hypothèse d'unitarité n'est en fait pas principale puisqu'une opération non unitaire impliquerait le même résultat.
Quelques portes de logiques quantiques
Une dernière étape est indispensable avant en premier lieuer le protocole de téléportation quantique. Il s'agit d'introduire les portes de logiques quantiques qui vont nous permettre de réaliser cette téléportation. En effet, la manipulation d'un qubit doit se faire par des opérations unitaires pour les raisons évoquées auparavant. Ainsi, l'opération logique associée à l'application d'une fonction 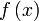 de la variable binaire x notée
de la variable binaire x notée 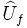 est définie par :
est définie par :
où x et y désignent respectivement les registres d'entrée et de sortie qui permettent effectivement d'avoir une opération unitaire puisque on vérifie aisément que 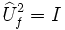 , sachant que
, sachant que  sert à désigner ici l'addition modulo 2 ("OU exclusif").
sert à désigner ici l'addition modulo 2 ("OU exclusif").
Voici enfin quelques exemples de portes. La porte cNOT (pour Control NOT) définie par
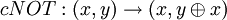 ,
,
et la porte d'Hadamard Hd dont l'action est la suivante
![H_{d}\vert x=0,1\rangle = \frac{1}{\sqrt{2}}\left[\vert 0\rangle + \left(-1\right)ˆ{x}\vert 1\rangle\right]](illustrations/3ee1cb242b3a4fafd8c7204fdea35445.png) .
.
Protocole de téléportation quantique
Nous arrivons enfin au vif du sujet à savoir le principe de la téléportation quantique. Il est de tradition d'appeler les protagonistes d'un scénario de communication Alice et Bob. Alice dispose d'un qubit 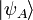 qu'elle souhaite transmettre à Bob. Elle dispose pour cela de deux canaux. Un canal classique et un canal quantique dit EPR, en référence au paradoxe Einstein-Podolsky–Rosen [1]. On précisera ultérieurement le sens d'une telle appellation quand on présentera la téléportation quantique dans le régime des variables continues. À ce stade, il suffit amplement de dire qu'il s'agit d'un canal composé de deux qubits maximalement intriqués, et dont l'état s'écrit :
qu'elle souhaite transmettre à Bob. Elle dispose pour cela de deux canaux. Un canal classique et un canal quantique dit EPR, en référence au paradoxe Einstein-Podolsky–Rosen [1]. On précisera ultérieurement le sens d'une telle appellation quand on présentera la téléportation quantique dans le régime des variables continues. À ce stade, il suffit amplement de dire qu'il s'agit d'un canal composé de deux qubits maximalement intriqués, et dont l'état s'écrit :
![\vert\phiˆ{+}_{AB}\rangle = \frac{1}{\sqrt{2}}\left[\vert 0_{A}0_{B}\rangle + \vert 1_{A}1_{B}\rangle \right] \neq \vert\phi_{A}\rangle\otimes\vert\phi_{B}\rangle](illustrations/fdb9688beac6baf7fb8d95e91c98eb82.png) .
.
En effet, pour un tel état, il est impossible de factoriser l'état de la paire de qubits sous la forme d'un produit tensoriel. Cette inséparabilité se traduit par de particulièrement fortes corrélations sur les résultats de mesure qu'il est impossible d'expliquer par des modèles classiques. On peut regarder à ce propos l'article sur l'expérience d'Aspect.
Alice qui souhaite communiquer à Bob l'état de son qubit sans être importunée par les indiscrétions d'Eve, applique à son qubit 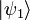 et au qubit de la part intriqué l'algorithme quantique suivant :
et au qubit de la part intriqué l'algorithme quantique suivant :
A) L'état d'origine du qubit d'Alice et de la paire intriquée s'écrit
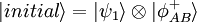 .
.
B) On fait interagir le qubit d'Alice avec le qubit EPR qu'elle détient via une porte cNOT dont le qubit de contrôle est le qubit d'Alice 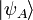 . L'état intermédiaire se met alors sous la forme suivante :
. L'état intermédiaire se met alors sous la forme suivante :
C) Par la suite, Alice fait subir à son qubit une opération d'Hadamard Hd qui donne le résultat final :
![\vert final\rangle = \frac{1}{2}\vert 0_{A}0_{A}\rangle\left[\alpha\vert 0_{B}\rangle + \beta \vert 1_{B}\rangle \right] + \frac{1}{2}\vert 0_{A}1_{A}\rangle\left[\beta\vert 0_{B}\rangle + \alpha \vert 1_{B}\rangle \right] + \frac{1}{2}\vert 1_{A}0_{A}\rangle\left[\alpha\vert 0_{B}\rangle - \beta \vert 1_{B}\rangle \right] + \frac{1}{2}\vert 1_{A}1_{A}\rangle\left[-\beta\vert 0_{B}\rangle + \alpha \vert 1_{B}\rangle \right]](illustrations/e27f5a69376b0434be2d827267b07ec1.png) .
.
On constate tandis que l'état du qubit d'Alice est téléporté sur le qubit de Bob dans 25 % des cas quand Alice mesure pour ces deux qubits les états binaires 0. Dans les autres cas, Alice doit transmettre à Bob le résultat de ces mesures, nommées mesures de Bell, pour que ce dernier puisse finaliser la téléportation. La théorie de la relativité restreinte d'Einstein n'est par conséquent pas violée puisque la communication des résultats des mesures de Bell se fait par un canal classique. En effet, on montre sans difficulté que les états de Bob correspondant à chaque possibilité sont semblables à l'état du qubit d'Alice à une opération unitaire près. A titre d'exemple, quand Alice projette ces deux qubits sur l'état  l'état de Bob se retrouve alors dans l'état
l'état de Bob se retrouve alors dans l'état 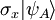 , où σx sert à désigner une des matrices de Pauli sur laquelle il est envisageable de décomposer tout opérateur hermitien (c'est-à-dire qu'une observable physique est représentée en physique quantique par un opérateur hermitien garantissant ainsi des valeurs propres réelles qui sont les grandeurs mesurables). Enfin, il faut souligner que le théorème de non-clonage quantique est respecté puisque le qubit d'Alice est totalement diminué lors des opérations et des mesures d'Alice. Ce schéma a été proposé en 1993 par Charles Bennett[2] (alors chez IBM) sous une autre forme plus générale consistant à projeter les EPR et qubits à téléporter sur des états intriqués nommés états de Bell. À
, où σx sert à désigner une des matrices de Pauli sur laquelle il est envisageable de décomposer tout opérateur hermitien (c'est-à-dire qu'une observable physique est représentée en physique quantique par un opérateur hermitien garantissant ainsi des valeurs propres réelles qui sont les grandeurs mesurables). Enfin, il faut souligner que le théorème de non-clonage quantique est respecté puisque le qubit d'Alice est totalement diminué lors des opérations et des mesures d'Alice. Ce schéma a été proposé en 1993 par Charles Bennett[2] (alors chez IBM) sous une autre forme plus générale consistant à projeter les EPR et qubits à téléporter sur des états intriqués nommés états de Bell. À
Premières réalisations expérimentales
L'une des premières réalisations expérimentales de la téléportation quantique en variables discrètes a été réalisée par l'équipe de Anton Zeilinger en 1997 [3]. Une paire de photons intriqués est créée par conversion paramétrique spontanée et dégénérée en fréquence dans un cristal non linéaire χ (2) . C'est une conversion de type II puisque l'accord de phase est assuré par biréfringence. L'impulsion de pompage est polarisée parallèlement à l'axe extraordinaire. Les photons signal et complémentaire sont alors émis suivant des polarisations orthogonales suivant deux cônes de fluorescence paramétrique. L'intersection de ces deux cônes conduit à des photons intriqués en polarisation qui sont en fait dans un état antisymétrique de Bell :
![\vert\psi_{23}ˆ{-}\rangle = \frac{1}{\sqrt{2}}\left[\vert h\rangle_{2}\vert v\rangle_{3}-\vert v\rangle_{2}\vert h\rangle_{3}\right]](illustrations/e1a6563effffd0fb7cfdc20aed3b9e8f.png) ,
,
où h et v désignent respectivement les états de polarisation horizontale et verticale. L'objectif de l'expérience est alors de projeter le photon à téléporter et le photon intriqué sur ce même état de Bell antisymétrique par des mesures de coïncidence à l'issue d'une lame séparatrice 50/50. En effet, les deux détecteurs de part et d'autre de la lame cliquent en même temps quand les deux photons sont soit simultanément transmis, soit simultanément réfléchis. On montre tandis que les photons peuvent être dans un état intriqué de la forme 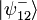 , ce qui suffit à assurer la téléportation puisque :
, ce qui suffit à assurer la téléportation puisque :
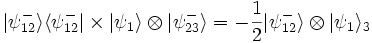 .
.
Le qubit de Bob se retrouve bien dans l'état du qubit d'Alice 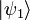 dans 25 % des cas. On doit le vérifier en plaçant un cube séparateur de polarisation orienté à +/- 45 ° comparé aux états de polarisations verticales et horizontales. Il y a téléportation pour la triple coïncidence à l'issue de la lame séparatrice d'Alice et sur la voie correcte du cube de Bob[4].
dans 25 % des cas. On doit le vérifier en plaçant un cube séparateur de polarisation orienté à +/- 45 ° comparé aux états de polarisations verticales et horizontales. Il y a téléportation pour la triple coïncidence à l'issue de la lame séparatrice d'Alice et sur la voie correcte du cube de Bob[4].
Téléportation quantique en variables continues
Aujourd'hui, ce protocole est implémenté en optique quantique dans le régime des variables dites continues par opposition au régime des variables discrètes abordé auparavant qui se définit entre autres par le comptage des photons. En effet, dans le régime des variables continues, on ne peut plus distinguer les photons individuellement : ils arrivent par «bouffées» contenant un très grand nombre de photons 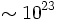 rendant l'approche par comptage totalement inimaginable !
rendant l'approche par comptage totalement inimaginable !
La première réalisation expérimentale d'une telle téléportation a été réalisée par l'équipe de H. J. Kimble au Caltech aux États-Unis par Akira Furusawa en 1998 [5].
Avant en premier lieuer le principe de cette expérience qui, actuellement est devenue routinière en optique quantique, il est utile de préciser quelques notions liées aux variables continues.
Expression d'un champ électrique monomode
Un champ électrique monomode s'écrit de manière classique comme :
qui est la décomposition usuelle du champ électrique dans le plan de Fresnel.
La procédure de quantification canonique conduit à associer au champ électrique l'opérateur suivant :
où les opérateurs 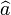 et
et 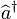 sert à désigner respectivement les opérateurs d'annihilation et de créations d'une excitation élémentaire d'énergie
sert à désigner respectivement les opérateurs d'annihilation et de créations d'une excitation élémentaire d'énergie 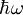 : le photon. Ils obéissent à la règle de commutation d'un oscillateur harmonique
: le photon. Ils obéissent à la règle de commutation d'un oscillateur harmonique ![\left[\widehat{a},\widehat{a}ˆ{\dagger}\right] = 1](illustrations/285c5ab5602b42bdfeb67369b974b623.png) .
.
La constante 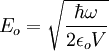 correspond au champ électrique associé à un seul photon dans une cavité cubique dont le volume de quantification est V.
correspond au champ électrique associé à un seul photon dans une cavité cubique dont le volume de quantification est V.
Opérateurs de quadrature
Ces opérateurs sont définis par ressemblance aux opérateurs de position et d'impulsion d'un oscillateur harmonique régi par les opérateurs de création et d'annihilation introduit auparavant. Ils seront définis généralement, en tenant compte d'une éventuelle rotation d'angle θ dans le plan de Fresnel, comme :
Pour le cas spécifiques θ = φ, ces opérateurs correspondent respectivement aux quadratures d'amplitude et de phase du champ. Ainsi, leurs variances caractérisent respectivement les fluctuations d'amplitude et de phase. De plus, il est facile de vérifier que ces opérateurs ne commutent pas puisque
![\left[\widehat{p}_{\theta},\widehat{q}_{\theta} \right] = 2i](illustrations/02ba38324001359d7c32ac1bbe999b75.png) .
.
On en déduit alors l'inégalité d'Heisenberg suivante :
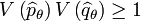 ,
,
qui est fréquemment employée sous la forme :
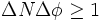 .
.
C'est à dire, quand on mesure avec précision le nombre de photons d'un faisceau, on brouille totalement la phase de ce dernier, et réciproquement.
Limite quantique standard et états cohérents du champ
L'opérateur d'annihilation 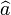 a pour vecteur propre :
a pour vecteur propre :
où α sert à désigner un nombre complexe lié à l'amplitude A ainsi qu'à la phase φ du champ par α = Aeiφ.
Or, l'action des opérateurs de création et d'annihilation sur les états de Fock (i. e. état nombre de photon où il y a précisément n photons dans le mode reconnu) 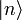 donne :
donne :
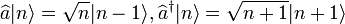 .
.
On vérifie alors aisément que :
Il est aussi utile de remarquer qu'un tel état cohérent du champ peut s'exprimer à partir de l'état vide de photons 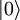 avec un opérateur déplacement
avec un opérateur déplacement
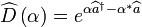 .
.
L'état cohérent, ou état quasi-classique de Glauber, s'écrira comme :
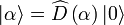 .
.
Ainsi, l'état vide de photons est un état cohérent dont la valeur moyenne de photons est nulle. Les fluctuations de cet état en amplitude et en phase définissent la limite quantique standard comparé à laquelle on repère toute variance de bruit,
On voit quoiqu'un état cohérent est affecté par des fluctuations qui sont semblables à celle du vide, puisqu'un état cohérent brillant n'est rien d'autres que l'état du vide déplacé dans le plan de Fresnel qu'on nomme aussi espace des phases.
Enfin, si on se rappelle l'inégalité d'Heisenberg qui contraint la mesure des quadratures d'amplitude et de phase, on constate qu'elle n'impose rien sur les variances individuelles. Il devient par conséquent envisageable d'imaginer des faisceaux dont les fluctuations peuvent être «comprimés» selon l'une ou l'autre des quadratures. Il s'agit des états comprimés du rayonnement qui prennent une place importante dans les expériences d'optique quantique.
Compression et Intrication de faisceaux
Dans cette section, nous allons établir le lien particulièrement simple existant entre la compression de deux faisceaux et l'intrication de ces derniers. Pour celà, on considère deux faisceaux comprimés en amplitude selon des quadratures orthogonales en incidence sur une lame séparatrice 50/50 (SP). On notera A1 et A2 ces faisceaux incidents, et Aa et Ab les faisceaux émergents. La relation d'entrée sortie de la lame séparatrice donne :
Si les faisceaux incidents sont comprimés de manière correcte, on trouve en termes des variances :
Dans le cas d'une compression en amplitude maximale (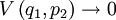 ), on obtient deux faisceaux idéalement corrélés en amplitude et anti-corrélés en phase. Il s'agit en fait de faisceaux EPR puisqu'une mesure sur l'un des faisceaux sert à déterminer l'état de l'autre même s'il est scindé spatialement du premier.
), on obtient deux faisceaux idéalement corrélés en amplitude et anti-corrélés en phase. Il s'agit en fait de faisceaux EPR puisqu'une mesure sur l'un des faisceaux sert à déterminer l'état de l'autre même s'il est scindé spatialement du premier.
Enfin, il existe deux méthodes remarquables pour produire des états comprimés. Il s'agit de l'effet Kerr et de l'augmentcation paramétrique. Dans le premier cas, l'effet Kerr modifie la forme du disque des fluctuations du vide en une ellipse oblique globalement comprimée en amplitude. Pour l'augmentcation paramétrique, la configuration la plus efficace est de se placer sous le seuil d'oscillation (i. e. les pertes de la cavité ne sont plus compensées par la pompe) et en dégénerescence de fréquence. On obtient alors du vide comprimé en sortie.
Réalisation expérimentale d'une téléportation quantique bipartite
Nous allons désormais aborder le principe de la téléportation quantique en variables continues comme l'illustre la figure.
Alice reçoit un faisceau d'amplitude complexe αin = xin + ipin dont elle souhaite transférer à Bob l'état des quadratures x et p sans ajout de bruit. Pour celà, elle combine le faisceau à téléporter sur une lame séparatrice 50/50 (SP) avec un des faisceaux intriqués (1). Alice mesure les quadratures de phase x et d'amplitude p (avec détection homodyne) à la sortie de la séparatrice (SP) :
Ces résultats sont ensuite transmis à Bob par l'intermédiaire de canaux classiques, ici des courants électriques directement proportionnels aux résultats des mesures. Bob effectue alors des modulations de phase (MP) et d'amplitude (MA), avec modulateurs électro-optiques surtout, sur un faisceau annexe qu'il a en sa disposition au préalable. Il combine ce faisceau modulé à l'autre faisceau intriqué (2) avec un miroir de particulièrement forte reflectivité (99 %). Bob dispose par conséquent d'un faisceau de sortie dont l'amplitude complexe s'écrira :
Enfin, si les faisceaux (1) et (2) sont idéalement intriqués :
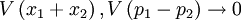 ,
,
le faisceau de sortie se retrouve précisément dans l'état du faisceau d'entrée :
On parle alors de téléportation quantique des quadratures du champ.
Critère de Téléportation Quantique
Il est indispensable d'introduire un critère pour juger de la qualité d'une téléportation. Il s'agit de la fidélité F définie par :
où 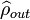 sert à désigner la matrice densité caractérisant l'état téléporté. On montre[6] que la fidelité de la téléportation est donnée par :
sert à désigner la matrice densité caractérisant l'état téléporté. On montre[6] que la fidelité de la téléportation est donnée par :
On constate que si on remplace les faisceaux EPR par des états cohérents, la fidélité atteint à peine 1/2 qui fixe la limite entre la téléportation classique utilisant des corrélations classiques et la téléportation quantique où le recours à l'intrication quantique est indispensable. D'autre part, une fidélité supérieure à 2/3 garantie l'unicité de la copie de Bob : aucune autre meilleure copie ne peut exister ! Il s'agit en fait d'une conséquence du théorème de non clonage quantique[7] qui est à la base de la sécurité de ce genre de protocole de communication quantique.
Enfin, la première tentative de A. Zeilinger ne forme pas vraiment une téléportation quantique comme l'ont remarqué H. J. Kimble et al dans un commentaire[8] de l'article d'origine. En effet, le calcul de la fidélité de cette téléportation conduit à une valeur de 1/2, ce qui ne correspond pas à une téléportation quantique. Il existe aussi une réponse des autrichiens à ce commentaire.
Vers les réseaux de communications quantiques : Téléportation quantique tripartite
Dans cette configuration, trois protagonistes interviennent : Alice, Bob et Claire. Ils partagent trois faisceaux intriqués 1, 2 et 3 dans un état dit de Greenberger - Horne - Zeilinger (GHZ). Ce canal se définit par les valeurs propres suivantes :
pour les mêmes combinaisons des opérateurs de quadratures.
On montre de la même manière que auparavant que cet état intriqué permet d'avoir une téléportation quantique entre Alice et Bob sous le contrôle de Claire[9]. Ainsi, quand le gain de la transmission entre Bob et Claire est nul, la téléportation est strictement classique et se retrouve même dégradée comparé à la fidélité limite de 1/2 caractérisant la frontière entre la limite classique et quantique où l'intrication devient indispensable.
Ce type de téléportation quantique peut être particulièrement intéressant en cryptologie quantique puisque Claire contrôle le transfert de l'information quantique entre Alice et Bob.
Conclusions et perspectives
Actuellement, on à pour but de produire ainsi qu'à téléporter le plus scrupuleusement envisageable des états fortement non classiques comme des superpositions d'états cohérents incompatibles : "chats de Schrödinger" ![\vert\psi\rangle = \frac{1}{\sqrt{2}}\left[\vert\alpha\rangle + \vert -\alpha\rangle\right]](illustrations/17464eb194a31caef3584f23ab34184d.png) ou des états intriqués. Dans ce dernier cas, on parle de "entanglement swapping" pouvant atteindre des fidélités de l'ordre de 0.75 [10] surpassant ainsi la valeur seuil de 2/3 liée au théorème de non clonage quantique. Enfin, le protocole de téléportation quantique s'inscrit dans une perspective plus ambitieuse consistant à la mise en œuvre de réseaux de communication quantique dans lesquelles on transfere l'état d'un dispositif quantique fragile sur une mémoire quantique plus robuste vis à vis de la décohérence[11]. D'intenses recherches se concentrent par conséquent sur la réalisation de ces relais quantiques mais également sur les possibilités d'augmenter ou de distiller l'intrication de canaux EPR qui sont infailliblement soumis à des pertes en lignes. À partir de plusieurs canaux EPR affaiblis qu'on distille, on obtient un plus petit nombre de canaux plus fortement intriqués, rendant la téléportation quantique plus efficace et plus sûre[12], [réf. souhaitée].
ou des états intriqués. Dans ce dernier cas, on parle de "entanglement swapping" pouvant atteindre des fidélités de l'ordre de 0.75 [10] surpassant ainsi la valeur seuil de 2/3 liée au théorème de non clonage quantique. Enfin, le protocole de téléportation quantique s'inscrit dans une perspective plus ambitieuse consistant à la mise en œuvre de réseaux de communication quantique dans lesquelles on transfere l'état d'un dispositif quantique fragile sur une mémoire quantique plus robuste vis à vis de la décohérence[11]. D'intenses recherches se concentrent par conséquent sur la réalisation de ces relais quantiques mais également sur les possibilités d'augmenter ou de distiller l'intrication de canaux EPR qui sont infailliblement soumis à des pertes en lignes. À partir de plusieurs canaux EPR affaiblis qu'on distille, on obtient un plus petit nombre de canaux plus fortement intriqués, rendant la téléportation quantique plus efficace et plus sûre[12], [réf. souhaitée].
Références
- Théorie :
- C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, & W. K. Wootters, Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels, Phys. Rev. Lett. 70 1895-1899 (1993) (document en ligne)
- G. Brassard, S Braunstein, R Cleve, Teleportation as a quantum computation, Physica D 120 43-47 (1998)
- G. Rigolin, Quantum teleportation of an arbitrary two qubit state and its relation to multipartite entanglement, Phys. Rev. A 71 032303 (2005) (document en ligne)
- A. Díaz-Caro, On the Teleportation of N-qubit States, arXiv quant-ph/0505009 (2005) (document en ligne)
- Premières expérimentations avec des photons :
- D. Bouwmeester, J. -W. Pan, K. Mattle, M. Eibl, H. Weinfurter, & A. Zeilinger, Experimental quantum teleportation, Nature 390, 6660, 575-579 (1997).
- D. Boschi, S. Branca, F. De Martini, L. Hardy, & S. Popescu, Experimental realization of teleporting an unknown pure quantum state via dual classical an Einstein-Podolsky-Rosen channels, Phys. Rev. Lett. 80, 6, 1121-1125 (1998) ;
- Premières expérimentations avec des atomes :
- M. Riebe, H. Häffner, C. F. Roos, W. Hänsel, J. Benhelm, G. P. T. Lancaster, T. W. Körber, C. Becher, F. Schmidt-Kaler, D. F. V. James, R. Blatt : Deterministic quantum teleportation with atoms, Nature 429, 734 - 737 (2004)
- M. D. Barrett, J. Chiaverini, T. Schætz, J. Britton, W. M. Itano, J. D. Jost, E. Knill, C. Langer, D. Leibfried, R. Ozeri & D. J. Wineland : Deterministic quantum teleportation of atomic qubits, Nature 429, 737
(en) Téléportation quantique à IBM (fr) Téléportation & explication d'une source à photons uniques au GAP (Université de Genève, Switzerland)
(fr) Soutenance d'un projet bibliographique du Parcours de Physique Quantique (ENS Paris) par Taoufik AMRI dont est inspiré en partie cet article sur wikipédia Fichier pdf (3.33 Mo)
Notes
- ↑ A. Einstein, B. Podolsky, N. Rosen, Can quantum-mechanical description of physical reality be considered complete ?. Phys. Rev. 41, 777 (1935)
- ↑ C. H. Bennett et al. Teleporting an unknown quantum state via dual classical and EPR channels. Phys. Rev. Lett. 70, 1895–1899 (1993)
- ↑ Anton Zeilinger. et al. Experimental quantum teleportation. Nature 390, 575–579 (1997)
- ↑ Soutenance d'un projet bibliographique de Taoufik AMRI dont cet article s'inspire fortement, Fichier pdf (3.33 Mo)
- ↑ A. Furusawa, H. J. Kimble et al.. Unconditional quantum teleportation. Science 282, 706–709 (1998)
- ↑ Soutenance d'un projet bibliographique de Taoufik AMRI dont cet article s'inspire fortement, Fichier pdf (3.33 Mo)
- ↑ F. Grosshans, P. Grangier. No-cloning theorem and teleportation criteria for quantum continuous variables. Phys. Rev. A 64, 010301 (2001), [1]
- ↑ H. J. Kimble et al., A posteriori teleportation, arXiv :quant-ph/9810001v1
- ↑ H. Yonezawa, T. Aoki, and A. Furusawa, Demonstration of a quantum teleportation network for continuous variables. Nature 431 (2004)
- ↑ H. Yonezawa, A. Furusawa et al. Phys. Rev. Lett. 99, 110503 (2007)
- ↑ cf. A. Dantan, N. Treps, A. Bramati and M. Pinard. Teleportation of an atomic ensemble quantum state. Phys. Rev. Lett. 94, 050502 (2005) ]
- ↑ En effet, une intrication plus forte implique une fidélité de téléportation plus grande, et si cette dernière dépasse la valeur seuil de 2/3, alors le théorème de non clonage quantique garantie que l'état téléporté est unique. (2007)
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

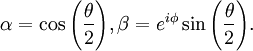
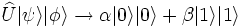
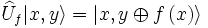
![\vert inter. \rangle =\frac{\alpha}{\sqrt{2}}\vert 0_{A}\rangle\left[\vert 0_{A}0_{B}\rangle + \vert 1_{A}1_{B}\rangle\right]+\frac{\beta}{\sqrt{2}}\vert 1_{A}\rangle\left[\vert 1_{A}0_{B}\rangle + \vert 0_{A}1_{B}\rangle\right]](illustrations/ae05974951a152a2c1da383b6b74a491.png)
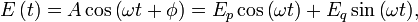
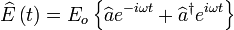
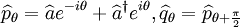
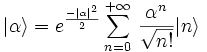
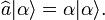
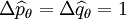
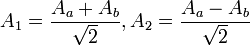
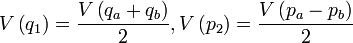
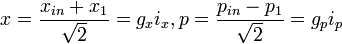
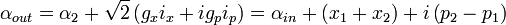
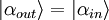
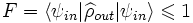
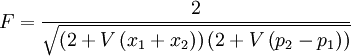

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité