Matrice densité
La matrice densité, ou opérateur densité est une entité mathématique introduite par le mathématicien et physicien John von Neumann.
Recherche sur Google Images :

Source image : fr.wikipedia.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- ... Les états quantiques sont des vecteurs indépendant du temps.... Comme la distribution de Wigner, la matrice densité est coûteuse en termes de ... de la physique et surtout en physique quantique statistique.... (source : s.correia.free)
- L'operateur, ou matrice, densite est l'outil qui sert à decrire toutes ces situations...... Exemple : Etat singulet d'un syst`eme de deux spins 1/2 :... Comme en physique classique, il existe en physique quantique de nombreuses situations... statistique qui s'introduit ici est de nature classique : il est lie... (source : coldatomsintoulouse)
- Les fameux Alice et Bob veulent téléporter un état quantique (a). On sup-...... car la dynamique des dispositifs ouverts transforme des états purs en mélange statistique....... Alors l'évolution de la matrice densité est ... (source : ens-lyon)
La matrice densité, ou opérateur densité est une entité mathématique introduite par le mathématicien et physicien John von Neumann. Elle sert à résumer en une seule matrice tout la totalité envisageable des états quantiques d'un dispositif physique donné à un instant donné, mariant ainsi mécanique quantique et physique statistique.
La description du dispositif se fait ici grâce à un vecteur d'état 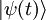 qu'on peut développer sur la base des
qu'on peut développer sur la base des 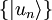 :
:
avec 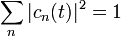
L'opérateur densité est défini pour un état pur par :
Mélange statistique d'états purs
En admettant qu'un certain dispositif physique puisse être, à un certain instant t, dans un mélange statistique (fini ou illimité) d'états quantiques 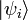 avec des probabilités pi (où
avec des probabilités pi (où  ), alors la matrice densité représentant la totalité de ces états est :
), alors la matrice densité représentant la totalité de ces états est :
L'aspect statistique introduit ici est de deux natures, l'une classique et l'autre quantique :
- 1. classique : dû à l'estimation du ket par une distribution statistique des différents kets envisageables,
- 2. quantique : incertitude quantique principale même si le dispositif est idéalement déterminé.
Les éléments de la matrice densité valent :
où 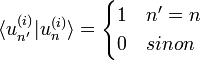 d'où
d'où 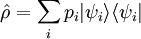
Propriété
La matrice obtenue a les propriétés suivantes :
- Elle est hermitienne,
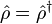 , elle peut par conséquent être diagonalisée, et ses valeurs propres sont positives.
, elle peut par conséquent être diagonalisée, et ses valeurs propres sont positives. - Sa trace est identique à 1,
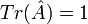 , conservation de la probabilité totale.
, conservation de la probabilité totale. - Elle doit être définie positive ou nulle.
- Dans le cas d'un état pur, l'opérateur densité est alors un projecteur :
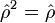 .
. 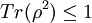 , avec identiqueité si et uniquement si le dispositif physique est dans un état pur (c'est-à-dire que l'ensemble des pi sont nuls sauf un).
, avec identiqueité si et uniquement si le dispositif physique est dans un état pur (c'est-à-dire que l'ensemble des pi sont nuls sauf un).
Valeur moyenne
On peut calculer la valeur moyenne d'une observable A à partir de la formule :
avec 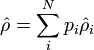 est la matrice densité d'un mélange statistique d'états.
est la matrice densité d'un mélange statistique d'états.
On considère un mélange statistique d'états :
- d'où :
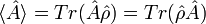
Evolution avec le temps
L'évolution temporelle de l'opérateur d'état est donné par l'équation de Schrödinger dépendante du temps :
Lien avec l'entropie
Enfin, on peut définir l'entropie de Von Neumann :
où kB est la constante de Boltzmann.
L'entropie d'un état pur est nul, car il y a aucune incertitude sur l'état du dispositif. On peut aussi trouver une base où la matrice est diagonale, avec des 0, et un 1 sur la diagonale, ce qui donne bien une entropie identique à 0.
Voir aussi
Bibliographie
- C. Cohen-Tannoudji, B. Diu et F. Laloë, Mécanique quantique [détail des éditions]
- Bernard Diu, Claudine Guthmann, Danielle Lederer et Bernard Roudet, Éléments de physique statistique, 1996 [détail des éditions]
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 13/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

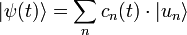
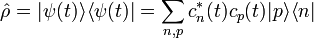
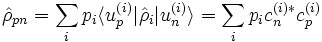
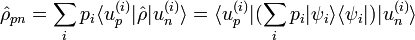
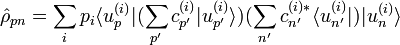
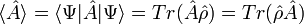

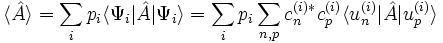
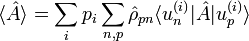
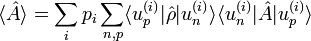

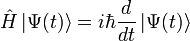
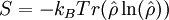

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité