Effet tunnel
L'effet tunnel sert à désigner la propriété que possède un objet quantique de franchir une barrière de potentiel, franchissement impossible selon la mécanique classique.
Recherche sur Google Images :

Source image : www.cnrs.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- L'effet tunnel est une des prédictions les plus étonnantes de la mécanique quantique.... En mécanique quantique, par contre, la fonction d'onde associée à cette... Figure 2.1 : Barrière de potentiel dans un modèle unidimensionnel.... (source : users.skynet)
- À toute onde on peut associer des particules : par exemple, ... C'est cette traversée de barrière de potentiel, sorte d'effet passe-muraille pour... L'effet tunnel est élastique. (Si on lance des électrons contre une barrière, ... (source : conspirovniscience)
- L'effet tunnel est à l'œuvre dans : les molécules : NH3, par exemple, ... Fonction d'onde d'un électron à travers une barrière de potentiel... (source : ilephysique)
L'effet tunnel sert à désigner la propriété que possède un objet quantique de franchir une barrière de potentiel, franchissement impossible selon la mécanique classique. Le plus souvent, la fonction d'onde d'une particule, dont le carré du module représente la densité de probabilité de présence, ne s'annule pas au niveau de la barrière, mais s'atténue au sein de la barrière, quasiment exponentiellement pour une barrière assez large. Si, à la sortie de la barrière de potentiel, la particule possède une probabilité de présence non nulle, elle peut traverser cette barrière. Cette probabilité dépend des états accessibles de part et d'autre de la barrière mais aussi de son extension spatiale.
Analyse
Au niveau théorique le comportement tunnel n'est pas principalement différent du comportement classique de la particule quantique face à la barrière de potentiel ; elle satisfait à l'équation de Schrödinger, équation différentielle impliquant la continuité de la fonction d'onde et de sa dérivée première dans tout l'espace. De même que l'équation des ondes électromagnétiques mène au phénomène des ondes évanescentes, de même la fonction d'onde rencontre des cas où l'amplitude de probabilité de présence est non nulle dans des lieux où l'énergie potentielle est supérieure à l'énergie totale.
Si, au niveau mathématique l'évaluation de l'effet tunnel peut quelquefois être simple, l'interprétation qu'on cherche à donner aux solutions révèle le fossé qui sépare la mécanique classique, domaine du point matériel suivant une trajectoire définie dans l'espace-temps, de la mécanique quantique où la notion de trajectoire simple disparaît au profit de tout un ensemble de trajectoires envisageables, dont des trajectoires où le temps apparaît complexe ou imaginaire pur... où les vitesses deviennent imaginaires.
On notera à ce propos que la durée de traversée tunnel d'une particule à travers une barrière quantique a été, et est toujours, le sujet d'âpres discussions. Des études assez nombreuses dans le domaine électromagnétique ou photonique ont révélé la naissance de ce qu'on peut interpréter comme des vitesses supraluminiques, respectant cependant la relativité restreinte : il s'agit du phénomène connu sous le nom d'effet Hartman.
Applications
L'effet tunnel est à l'œuvre dans :
- les molécules : NH3, par exemple,
- les modélisations des désintégrations (fission, radioactivité alpha),
- les transistors,
- certaines diodes,
- différent types de microscopes,
- l'effet Josephson.
Cas spécifique : l'effet tunnel résonnant.
Exemples
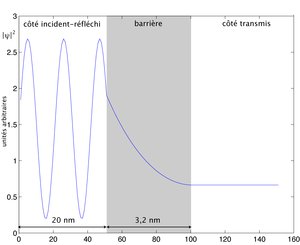
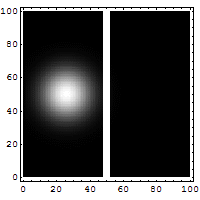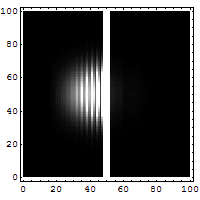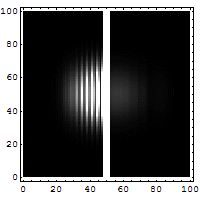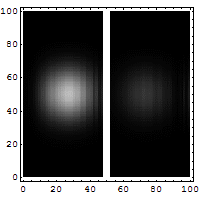
Une onde plane correspondant à une particule d'une masse effective de 0, 067 fois la masse de l'électron, d'énergie 0, 08 eV est incidente sur une barrière de potentiel rectangulaire simple, de 0, 1 eV. Le schéma révèle la densité de probabilité de présence associée à cet état stationnaire. Le côté gauche révèle le phénomène d'interférence entre l'onde incidente et l'onde réfléchie. La partie tunnel (dans la barrière) provient de la combinaison de deux exponentielles, respectivement décroissantes de gauche à droite, et de droite à gauche. À droite, l'onde plane transmise se révèle par une densité de probabilité de présence constante.
Fonction d'onde d'un électron, représentant la densité de probabilité de sa position. La plus grande probabilité est que l'électron "rebondisse". Il existe une faible probabilité que l'électron franchisse la barrière de potentiel.
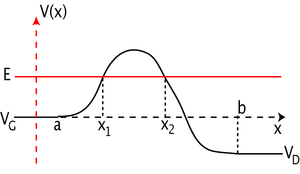
La barrière quantique sépare l'espace en trois, dont les parties gauche et droite sont reconnues comme ayant des potentiels constants jusqu'à l'infini (VG à gauche, VD à droite). La partie intermédiaire forme la barrière, qui peut être compliquée, révélant un profil doux, ou au contraire constitué de barrières rectangulaires, ou autres peut-être en séries.
On s'intéresse fréquemment à la recherche des états stationnaires pour de telles géométries, états dont l'énergie peut être supérieure à la hauteur de potentiel, ou au contraire inférieure. Le premier cas correspond à une situation dénommée quelquefois comme classique, quoique la réponse révèle un comportement typiquement quantique ; le second correspond au cas où l'énergie de l'état est inférieure à la hauteur du potentiel. La particule à laquelle correspond l'état traverse alors la barrière par effet tunnel, ou, c'est à dire, si on considère le diagramme énergétique, par effet saute-mouton.
Envisageant une particule incidente depuis la gauche, l'état stationnaire prend la forme simple suivante :
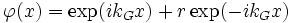 pour x < a;
pour x < a;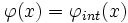 pour
pour 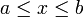 ;
;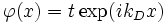 pour
pour 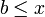 ;
;
où r et t sont respectivement les cœfficients de réflexion et transmission en amplitude pour l'onde plane incidente 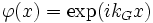 .
. 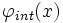 est la fonction d'onde au sein de la barrière, dont le calcul peut être assez compliqué ; elle est liée aux expressions de la fonction d'onde dans les demi-espaces droits et gauches par les relation de continuité de la fonction d'onde et de sa dérivée première.
est la fonction d'onde au sein de la barrière, dont le calcul peut être assez compliqué ; elle est liée aux expressions de la fonction d'onde dans les demi-espaces droits et gauches par les relation de continuité de la fonction d'onde et de sa dérivée première.
Assez fréquemment on s'intéresse à la probabilité de transmission (donnant lieu au courant tunnel, par exemple), et par conséquent on privilégie l'étude du cœfficient de transmission t, plus exactement la valeur en amplitude et phase du cœfficient 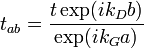 , caractérisant les relations entre l'onde plane incidente, prise à l'entrée a et l'onde plane de sortie prise au point b. La probabilité de transmission est appelée la transmittivité T = | tab | 2.
, caractérisant les relations entre l'onde plane incidente, prise à l'entrée a et l'onde plane de sortie prise au point b. La probabilité de transmission est appelée la transmittivité T = | tab | 2.
Ce sont ces transmittivités qui sont présentées dans quelques cas spécifiques ci-dessous, limitées (en fait pour certaines formules uniquement) au cas tunnel.
La plupart des particularités de l'effet tunnel apparaissent lors de la considération de la barrière de potentiel la plus simple, une barrière rectangulaire symétrique, pour laquelle le potentiel est constant (égal à U) entre les points a et b, et nul à droite ainsi qu'à gauche. Dans ce cas les vecteurs d'onde incident (réfléchi) et transmis ont même module, noté 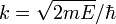 alors que la partie intérieure de la fonction d'onde est de la forme AeKx + Be − Kx avec
alors que la partie intérieure de la fonction d'onde est de la forme AeKx + Be − Kx avec 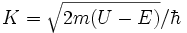 .
.
Pour les calculs on se place dans le repère ou a = 0. La condition de continuité en 0 de la fonction d'onde et de sa dérivée s'écrit :
La condition de continuité en b :
De ces équations on évalue les complexes r, t et la transmittivité :
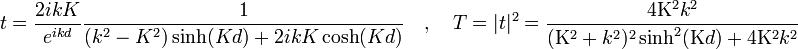 ,
,
avec d = b − a l'épaisseur de la barrière.
Dans le cas de barrière épaisse (Κd grand), on obtient la formule simple à retenir :
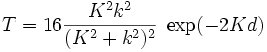 .
.
Dans ce cas là, on considère généralement la transmittivité comme le produit obtenu par l'approche BKW (cf. infra le terme exponentiel) par un préfacteur qui n'est que le produit des modules carrés des cœfficients de transmission propres aux interfaces d'entrée et de sortie.
Cette structure est une forme simplifiée de celle qui apparaît dans le cas d'une barrière de forme quelconque décomposée comme une série de barrières rectangulaires. La structure du calcul repose alors sur la prise en compte d'une écriture matricielle des équations, reliant les composantes progressive et régressive dans chaque couche, donnant la possibilité l'établissement de la matrice de transfert du mode stationnaire entre l'espace d'entrée et l'espace de sortie.
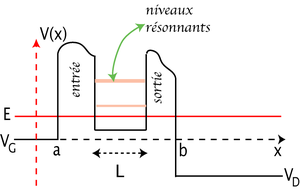
Cette méthode est illustrée sur le cas d'une structure rencontrée en électronique ou optique, la barrière tunnel résonnante, constituée d'une barrière d'entrée d'une partie interne de potentiel bas (puits de potentiel, de largeur L) et d'une barrière de sortie (cf. schéma). On montre que, dans le cas où le potentiel dans le puits est constant (définissant un vecteur d'onde réel 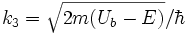 ), la transmittivité de la barrière peut s'écrire :
), la transmittivité de la barrière peut s'écrire :
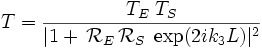 ;
;
dans le numérateur apparaissent les transmittivités des barrières d'entrée et de sortie, et le dénominateur contient, hormis les cœfficients de réflexion en amplitude des barrières d'entrée de sortie, vues depuis l'intérieur du puits central, un terme exponentiel dont les variations (en fonction de l'énergie et/ou l'épaisseur) sont sources de résonances envisageables (la formule est bonne pour des formes quelconques des barrières d'entrée et de sortie).
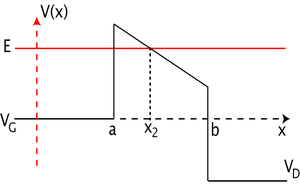
barrière trapézoïdale
La barrière trapézoïdale est obtenue par l'application d'une différence de potentiel entre les deux extrêmités de la barrière rectangulaire simple. Ce qui donne le schéma suivant, qui offre l'avantage d'admettre des solutions analytiques exactes ; en effet, pour cette barrière l'expression de la fonction d'onde, à l'intérieur est une combinaison linéaire de fonctions d'Airy, Ai et Bi, qu'on peut raccorder aux ondes planes solutions dans les parties gauches et droites.
Un cas spécifique apparaît dans le cadre de cette description. Si la différence de potentiel est suffisamment importante pour que la barrière montre l'existence d'un point classique de retour (passage d'une partie tunnel à une partie classique, au point x2), on obtient alors l'effet d'émission de champ, fréquemment utilisé en microscopie électronique. La particule, localisée en dans la bande de conduction à gauche, traverse par effet tunnel et se trouve accélérée vers l'extérieur, à droite.
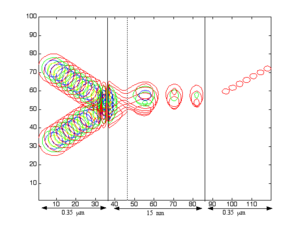
Peut-être, selon les valeurs de l'énergie et la forme de la barrière, des résonances de transmittivité peuvent apparaître, dues au saut de potentiel sur la marche de droite. Cette résonance a certains traits communs avec ceux de l'effet Ramsauer. Le schéma ci-contre correspond à une accumulation d'instantanés de la densité de présence associée à un paquet d'onde incident depuis le bas à gauche. L'effet de résonance se manifeste ici par la naissance des trois maxima dans la partie classique de la barrière. Au terme de la traversée les parties réfléchies et transmises s'éloignent vers le haut de la figure, à gauche ainsi qu'à droite respectivement.
approximation BKW
Dans le cas où la barrière de potentiel présente un profil doux, il est envisageable de montrer, à partir de l'équation de Schrödinger, ou à partir d'une discrétisation fine du potentiel en une série de petites barrières rectangulaires successives, que la fonction d'onde, en un point de coordonnée x dans la barrière peut s'écrire :
Cette approximation, étudiée par Brillouin, Kramers et Wentzel, est manifestement non valide pour les points classiques de retour, 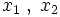 (cf. schéma), où le potentiel V (x) est identique à l'énergie E de l'état (k (x) est alors nul), il faut procéder avec quelque soin au raccordement de part et d'autre de ces points.
(cf. schéma), où le potentiel V (x) est identique à l'énergie E de l'état (k (x) est alors nul), il faut procéder avec quelque soin au raccordement de part et d'autre de ces points.
Dans le cadre de l'étude de la transmittivité cette expression est en particulier utile dans le cas tunnel, où k (x) devenant imaginaire pur, les deux exponentielles apparaissant dans l'expression ci-dessus correspondent à des termes décroissant de la gauche vers la droite (terme facteur de la constante A) et décroissante de la droite vers la gauche (terme facteur de B). Dans le cas d'une onde incidente venant de gauche, et pour les barrières suffisamment larges, la source de la partie régressive (expression B) est minime. La transmittivité due à cette partie tunnel est alors obtenue par la considération de la diminution de l'amplitude de l'onde entre les points classiques de retour d'entrée et de sortie, soit :
C'est cette expression qu'il faut alors calculer, par la méthode du potentiel inversé, par exemple. Cette approximation doit être corrigée par des préfacteurs, caractéristiques des potentiels à forte pente (saut de potentiel), qu'on rencontre à l'interface entre deux matériaux, et qui sont monnaies courantes dans les composants électroniques actuels (puits quantiques).
Approche semi-classique et utilisation du potentiel retourné
Antérieurement au développement des moyens de calculs rapides et puissants, qui permettent des évaluations précises des transmittivités, des méthodes approchées se sont développées qui ont permis, de façon efficace, de découvrir des caractéristiques de quelques transmittivités tunnel de certaines barrières d'importance théorique et pratique : barrière de type coulombien (modèle de radioactivité alpha) ou barrière triangulaire associée à l'effet de champ.
Il s'agit d'évaluer l'argument de l'exponentielle apparaissant dans l'approximation BKW. Il est aisé de calculer les intégrales pour les potentiels hyperboliques ou linéaires, mais il est intéressant de noter l'approche envisageable par la méthode du potentiel retourné pour laquelle l'évaluation de ![\exp [i \intˆx p(u)du/ \hbar]](illustrations/ffa1670efe14778bcdae97d14cb114d6.png) est obtenue via celle de
est obtenue via celle de ![\exp-[ S(E)/2\hbar]](illustrations/b8662a5b8ecb44d8ae9bcb7898755ed4.png) dans laquelle S (E) est l'action calculée sur l'orbite classique que suivrait une particule de même énergie dans le potentiel retourné, obtenu dans le cadre de l'emploi de la symétrie de Corinne.
dans laquelle S (E) est l'action calculée sur l'orbite classique que suivrait une particule de même énergie dans le potentiel retourné, obtenu dans le cadre de l'emploi de la symétrie de Corinne.
L'intérêt repose alors sur le fait que pour les barrières suffisamment épaisses, correspondant à des puits larges, l'action est , dans l'approximation semi-classique, sujette à la quantification 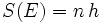 .
.
La transmittivité BKW d'une telle barrière s'écrit alors :
où le nombre quantique n (E) est la fonction réciproque de l'énergie E postulée comme niveau d'énergie discret du puits de potentiel correspondant à la barrière retournée.
Application à la radioactivité alpha
La barrière de potentiel que doit traverser la particule alpha, d'énergie E, après son apparition aléatoire au sein du noyau de numéro atomique Z, est transformée en un puits coulombien, dont les niveaux d'énergies sont ceux d'un hydrogénoïde. Ceci permet le calcul du nombre n (E) directement à partir de formules bien connues :
où apparaissent la masse réduite, et les charges de la particule alpha et du noyau fils (numéro atomique Z-1).
Le report du nombre n (E) dans l'expression de la transmittivité révèle alors le comportement observé de la demi-vie (proportionnelle à l'inverse de la transmittivité) des émetteurs alpha selon 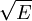 , énergie de la particule rencontrant la barrière.
, énergie de la particule rencontrant la barrière.
Application à l'effet Fowler-Nordheim
Sous l'action d'un champ électrique F, on peut faire sortir des électrons d'un métal (charge q, masse m, énergie E comparé au bas de la bande de conduction), surtout d'un métal alcalin de travail de sortie Φ. L'électron est alors soumis à un potentiel triangulaire qui peut, en première approximation, être traité par la méthode BKW : la transmittivité qui s'en déduit (compte tenu des points classiques de retour x1 = 0 et x2 = (Φ − E) / qF) ) est
L'obtention du courant tunnel doit évidemment tenir compte de la distribution en énergie et direction de la totalité des électrons de la bande, pour la température du conducteur.
Ici aussi la transmittivité aurait pu être obtenue en utilisant un potentiel retourné. Il s'agit alors du demi-puits de Torricelli, dont les niveau d'énergie peuvent être calculés et permettre l'obtention du nombre n (E).
- C. Cohen-Tannoudji, B. Diu et F. Laloë, Mécanique quantique [détail des éditions]
- Albert Messiah, Mécanique quantique [détail des éditions]
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

![\left\{\begin{array}{c} A = \frac{1}{2}[1+r+\frac{ik}{K}(1-r)] \\ B = \frac{1}{2}[1+r-\frac{ik}{K}(1-r)] \end{array}\right.](illustrations/960092f551dcba7cfa8ac28753d667cf.png)
![\left\{\begin{array}{c} A = \frac{t}{2}[1+\frac{ik}{K}]eˆ{ikb-Kb} \\ B = \frac{t}{2}[1-\frac{ik}{K}]eˆ{ikb+Kb} \end{array}\right.](illustrations/3f50cf795c9a8a150ab906618ac9909d.png)
![\varphi_{BKW}(x)=\frac{1}{\sqrt{k(x)}}\;[A\;\exp(i\intˆx\,du\,k(u))\;+\;B\;\exp(-i \intˆx\,du\,k(u))].](illustrations/c77a7e4e386136c0d9594cf8c8e61b33.png)
![T_{BKW}=\exp[-2\;\int_{x_1}ˆ{x_2}\;du\;\Kappa(u)]\quad ;\quad \Kappa(u)=\sqrt{\frac{2m}{\hbarˆ2}(V(u)-E)}\;.](illustrations/67cc904fb4ed284772b2808576cceefa.png)
![T(E) = \exp[-2\pi n(E)]\,,](illustrations/545bead451de30405c291d7db07a1735.png)
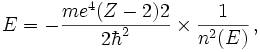
![T_{BKW}=\exp[-2\;\int_{x_1}ˆ{x_2}\;du\;\Kappa(u)]\;=\;\exp[-2\;\frac{\sqrt{2m}}{\hbar qF}\int_{0}ˆ{\Phi-E}\;dX\;\sqrt{X}]](illustrations/af2b73b70f8ee435bdb64c48ca19e509.png)
![\qquad=\exp[-\;\frac{4\sqrt{2m}}{3\hbar qF}(\Phi-E)ˆ{3/2}]\;.](illustrations/dc09c196c894e9918bf111e9dd94b6bc.png)

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité