Facteur de Landé
En mécanique quantique, le facteur de Landé est une grandeur physique sans dimension qui sert à relier le moment magnétique au moment cinétique d'un état quantique.
Recherche sur Google Images :
Source image : www.u-picardie.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- auteurs Uniquement lorsque on rédigé le moment magnétique de spin du neutron on a : M... Tout comme le facteur de Landé est le résultat de la composition de L avec S... (source : forums.futura-sciences)
- facteur de Landé du spin de l'électron (2). L'atome d'argent présente un moment cinétique orbital nul et un spin 1/2. Son facteur de Landé est 2, ... (source : lpm.u-nancy)
- Une relation entre la théorie du spin de l'électron et le tétraèdre régulier.... Le facteur de Landé est 2 augmenté de 0003; ici le facteur est précisément 2.... précisément 2 lorsque on compare le moment cinétique propre s et le moment... (source : er.uqam)
En mécanique quantique, le facteur de Landé est une grandeur physique sans dimension qui sert à relier le moment magnétique au moment cinétique d'un état quantique. Il est principalement utilisé dans le cas d'une particule de spin non nul.
Il est ainsi appelé en l'honneur d'Alfred Landé qui l'a introduit en 1921.
Au moment cinétique orbital d'une particule de charge q et de masse m est associé un moment magnétique orbital :
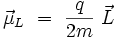 ,
,
où
- q/2m est le rapport gyromagnétique qui est le même que dans le cadre de la mécanique classique ;
- L est le moment cinétique orbital ;
- μL est le moment magnétique orbital.
Moment magnétique de spin
Cependant, dans le cas d'une particule principale, les moments cinétique et magnétique de spin, ne sont plus dans un rapport qui ne dépende que de la charge et de la masse, et on introduit un nombre sans dimension, g, facteur de Landé qui permette d'écrire
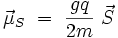 ,
,
où
- S est le spin ;
- μS est le moment magnétique de spin.
L'équation de Schrödinger ne fait pas intervenir le spin des particules, de sorte que la mécanique quantique non relativiste ne permet pas de déduire la valeur du facteur de Landé d'une particule de spin non nul. Une théorie plus précise, l'équation de Dirac, qui décrit les fermions relativistes de spin 1/2, prédit une valeur ge = −2 pour l'électron particulièrement proche de la valeur expérimentale est −2, 0023, et l'écart entre les deux est idéalement expliquée dans le cadre de l'électrodynamique quantique.
| particule | g | Δg |
|---|---|---|
| électron | −2, 002 319 304 3718 | 0, 000 000 000 0075 |
| neutron | −3, 826 085 46 | 0, 000 000 90 |
| proton | +5, 585 694 701 | 0, 000 000 056 |
| muon | −2, 002 331 8396 | 0, 000 000 0012 |
Atome
Pour un atome, le facteur de Landé intervient dans le calcul des niveaux d'énergie atomiques en champ magnétique faible.
Moment électronique
Si on s'intéresse au moment cinétique électronique J somme du spin électronique S et du moment cinétique orbital L, le facteur de Landé vaut :
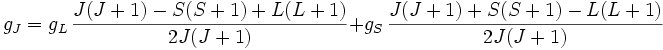 ,
,
soit approximativement
avec
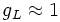 ;
;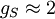 .
.
Le calcul du spin S ne fait intervenir que les électrons de valence.
Moment total
Si on s'intéresse au moment cinétique total de l'atome F, somme du spin nucléaire I et du moment cinétique électronique J, le facteur de Landé s'écrit
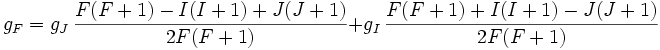 ,
,
soit approximativement
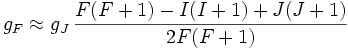 .
.
La simplification provient de l'approximation
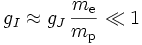 .
.
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 12/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

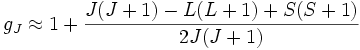

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité